Applications de la dérivation.
Dérivée et variation d'une fonction.
- Si $f$ est constante sur $I$ alors pour tout réel $x\in I$ on a: $f^{'}(x)=0$.
- Si $f$ est croissante sur $I$ alors pour tout $x\in I$ on a: $f^{'}(x)\geq 0$.
- Si $f$ est décroissante sur $I$ alors pour tout $x\in I$ on a:$f^{'}(x)\leq 0$.
- On a: $f'(-5)=f'(-4)=f'(0)=f'(2)=0$, les tangentes sont horizontales.
- et $f'(-7)=-3$ et $f'(5)=-2$.
Exemples d'étude de variations de fonctions.
Théorème.
Soit $f$ une fonction dérivable sur un intervalle $I$ de $\mathbb{R}$.- Si la fonction dérivée $f^{'}$ est nulle sur $I$ alors $f$ est constante sur $I$.
- Si la fonction dérivée $f^{'}$ est strictement positive sur $I$, sauf éventuellement en des points isolés où elle s'annule, alors $f$ est strictement croissante sur $I$.
- Si la fonction dérivée $f^{'}$ est strictement négative sur $I$, sauf éventuellement en des points isolés où elle s'annule, alors $f$ est strictement décroissante sur $I$.
Exemple.
Etudions les variations de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\dfrac{x}{1+x^2}$.
- Calculer $f'(x)$ en fonction de $x$.
- Etudier le signe de $f'(x)$ et en déduire les variations de la fonction $f$.
- Déterminer l'équation de $\mathcal{T}$, la tangente à la courbe $\mathcal{C}_f$ au point d'abisse $0$.
- Tracer $\mathcal{C}_f$ et $\mathcal{T}$.
Correction:
- $f(x)=\dfrac{u(x)}{v(x)}$ avec $u(x)=x$ et $v(x)=1+x^2$.
$f'(x)=\dfrac{u'(x)\times v(x)-u(x)\times v'(x)}{[v(x)]^2}$ $=\dfrac{1\times(1+x^2)-x\times(2x)}{(1+x^2)^2}$ $=\dfrac{1+x^2-2x^2}{(1+x^2)^2}$ $=\dfrac{1-x^2}{(1+x^2)^2}$ $=\dfrac{(1-x)(1+x)}{(1+x^2)^2}$.- Nous savons que: $(1+x^2)^2>0$ pour tout $x\in\mathbb{R}$.
- Le signe de $f'(x)$ est celui de $(1-x)(1+x)$, nous avons le tableau de signes ci-contre:
$1-x=0$ $\Leftrightarrow$ $x=1$.
$1+x=0$ $\Leftrightarrow$ $x=-1$.
- $(\mathcal{T}):y=f'(0)(x-0)+f(0)$.
$f'(x)=\dfrac{(1-x)(1+x)}{(1+x^2)^2}$, donc $f'(0)=\dfrac{(1-0)(1+0)}{(1+0^2)^2}=1$.
et $f(0)=\dfrac{0}{1+0^2}=0$. Donc $(\mathcal{T}):y=1\times(x-0)+0=x$.
Dérivée et extrema d'une fonction.
- pour un maximum local nous avons pour tout $x\in J\subset I$ $f(x)\leq f(a)$.
- pour un minimum local nous avons pour tout $x\in J\subset I$ $f(x)\geq f(a)$.
- Soit $f$ une fonction dérivable sur un intervalle $I$ ouvert de $\mathbb{R}$ et soit $a$ un réel appartenant à $I$.
Si $f$ admet un extremum local en $a$, alors $f^{'}(a)=0$. - Soit $f$ une fonction dérivable sur un intervalle $I$ ouvert de $\mathbb{R}$ et soit $a$ un réel appartenant à $I$.
Si la dérivée $f^{'}$ de $f$ s'annule en $a$ en changeant de signe, alors $f$ admet en $a$ un extremum local. - Montrons que $PC=\dfrac{x-x^2}{1+x}$.
Nous sommes en présence d'une configuration de thalés. En effet le triangle $MNB$ les droites $(MB)$ et $(PC)$ sont parrallèles.
On a: $\dfrac{NP}{NM}=\dfrac{NC}{NB}=\dfrac{PC}{MB}$.- Nous savons que $AM=x$, donc $MB=1-x$, avec $0\leq x\leq 1$.
- Nous savons aussi que $NC=x$ et $NB=1+x$, avec $0\leq x\leq 1$.
Donc $PC=\dfrac{x(1-x)}{1+x}=\dfrac{x-x^2}{1+x}$ pour tout $0\leq x < 1$.
Regardons pour $x=1$. Si $x=1$, on remarque que $PC=0$ et si $x=0$ alors $\dfrac{x(1-x)}{1+x}=0$. Donc pour tout $0\leq x\leq 1$ on a $PC=\dfrac{x-x^2}{1+x}$. - $f(x)=\dfrac{x-x^2}{1+x}=\dfrac{u(x)}{v(x)}$ avec $u(x)=x-x^2$ et $v(x)=1+x$ pour tout $x\in[0;1]$.
- $x\to x-x^2$ est dérivable sur $\mathbb{R}$, donc la fonction $u$ est dérivable sur $[0;1]$.
- De même $x\to x+1$ est dérivable sur $\mathbb{R}$, donc la fonction $v$ est dérivable sur $[0;1]$
- De plus pour tout $x\in [0;1]$, $v(x)=x+1\not=0$.
$f'(x)=\dfrac{(1-2x)\times(1+x)-(x-x^2)\times 1}{(1+x)^2}$ $=\dfrac{1-x-2x^2-x+x^2}{(1+x)^2}$ $=\dfrac{1-2x-x^2}{(1+x)^2}$.
Etudions le signe de $f'(x)$, comme $(1+x)^2>0$ pour tout $x\in\mathbb{R}$, il est clair que:
le signe de $f'(x)$ est celui de $1-2x-x^2=-x^2-2x+1$.
$\Delta=(-2)^2-4(-1)(1)=8>0$, donc les racines de $-x^2-2x+1$ sont:
$x_1=\dfrac{2-\sqrt{8}}{-2}=-1+\sqrt{2}\approx 0,4142$ et $x_2=\dfrac{2+\sqrt{8}}{2}=-1-\sqrt{2}$.
En nous restreignant à l'intervalle $[0;1]$, on a le tableau de variations de $f$.
$f(\sqrt{2}-1)=\dfrac{(\sqrt{2}-1)-(\sqrt{2}-1)^2}{(\sqrt{2}-1)+1}$ $=\dfrac{(\sqrt{2}-1)-(3-2\sqrt{2})}{(\sqrt{2}-1)+1}$ $=\dfrac{3\sqrt{2}-4}{\sqrt{2}}=3-2\sqrt{2}\approx 0,1716$.

la fonction $f$ admet un maximum égal à $3-2\sqrt{2}$ atteint pour $x=\sqrt{2}-1$.
$PC_{max}\approx 0,1716$. - Montrer que $PC=\dfrac{x-x^2}{1+x}$.
- Etudier les variations de $f$ définie sur $[0;1]$ par $f(x)=\dfrac{x-x^2}{1+x}$.
- Déduiser du tableau de variation de $f$, la valeur de $x$ pour laquelle la distance $PC$ est maximale.
Etude des fonctions rationnelles.
Définition.
On appelle une fonction rationnelle $f$ une fonction défine par $f(x)=\dfrac{P(x)}{Q(x)}$, où les fonctions $P$ et $Q\not=0$ sont deux fonctions polynômiales.
Méthode pour l'étude d'une fonction rationnelle.
- Rechercher le domaine de définition $\mathcal{D}_f$, on a: $\mathcal{D}_f=\bigg\{x\in\mathbb{R},~~ tels~~ que~~ Q(x)\not=0\bigg\}$
- Calculer $f'(x)=\dfrac{P'(x)\times Q(x)-P(x)\times Q'(x)}{[Q(x)]^2}$.
- Etudier le signe de $f'(x)$: comme $[Q(x)]^2>0$ pour tout $x\in\mathcal{D}_f$, il suffit d'étudier le signe du polynome $P'(x)\times Q(x)-P(x)\times Q'(x)$.
- Dresser le tableau de variation de $f$. Calculer les extrema relatifs éventuels de $f$.
- Tracer à l'aide d'un tableau de valeur la courbe $\mathcal{C}_f$ représentative de $f$.
Je m'entraine et je me teste!
- Je veux étudier par exemple $f(x)=\dfrac{1+2x-\dfrac{1}{3}x^2}{2-x}$, c'est bien une fonction rationnelle!
- Je réalise la méthode ci-contre, puis à la fin de mon travail je rentre les coefficients comme ci-dessous, pour vérifier.

Exemple.
Soit la fonction $f(x)=\dfrac{1+\dfrac{3}{2}x+x^{2}}{1+x}$.
- Déterminer le domaine de définition de $f$ ($\mathcal{C}_f$).
- Calculer $f'(x)$ en fonction de $x$.
- Etudier le signe de $f'(x)$ et en déduire les variations de la fonction $f$.
Etude de la fonction de $f(x)=\dfrac{1 +\dfrac{3}{2}x+x^{2}}{1+x}$
- $f(x)$ existe $\Leftrightarrow$ $1+x\not=0$ $\Leftrightarrow$ $x\not=-1$.
On dit que $-1$ est valeur interdite, la fonction f est definie sur $\mathbb{R}-\{-1\}$. - Calculons la fonction $f'(x)$, on a:
$f'(x)=\dfrac{u'(x)\times v(x)-u(x)\times v'(x)}{[v(x)]^2}=$ $=\dfrac{(\dfrac{3}{2}+2x)(1+x)-(1+\dfrac{3}{2}+x^2)}{(1+x)^2}=\dfrac{\dfrac{1}{2}+2x+x^{2}}{{\bigg(1+x\bigg)}^2}$ pour tout $x\in\mathbb{R}-\{-1\}$.
Etudions le signe de $f'(x)$, pour cela étudions le signe du polynôme $\dfrac{1}{2}+2x+x^{2}$
$\Delta=2^2-4\times\dfrac{1}{2}\times 1=+2$. Donc le trinôme du second degré $\dfrac{1}{2}+2x+x^{2}$ admet deux racines distinctes réelles:
$x_0=\dfrac{-2-\sqrt{+2}}{2}=-1 -\dfrac{1}{2}\sqrt{2}$
$x_1=\dfrac{-2+\sqrt{+2}}{2}=-1 +\dfrac{1}{2}\sqrt{2}$
$ \Delta>0$, donc le signe de $ +\dfrac{1}{2}+2x+x^{2}$ est du signe de $ a=+1$ à l'extérieur des racines.
Ici $ a$ est de signe +.
Comme $(1+x)^2>0$ pour tout $\mathbb{R}-\{-1\}$, le signe de $f'(x)$ est celui de $\dfrac{1}{2}+2x+x^{2}$. Nous avons donc le tableau de signes suivant: - Une asymptôte verticale $x=-1$ "la courbe ne pourra pas traverser cette droite".
- Une asymptôte verticale $y=x+\dfrac{1}{2}$. On remarque que $f(x)=(\dfrac{1}{2}+x)+\dfrac{\dfrac{1}{2}}{1+x}=(x+\dfrac{1}{2})+\dfrac{1}{2(x+1)}$
Tableau de variation de $f$.
x $-\infty$ $-1 -\dfrac{1}{2}\sqrt{2}$ $-1$ $-1 +\dfrac{1}{2}\sqrt{2}$ $+\infty$ signe de f'(x) + 0 - || - 0 + Variation de f $ \nearrow$ 0 $\searrow$ || $\searrow$ 0 $ \nearrow$
Calcul des extrema locaux .
$f(-1 -\dfrac{1}{2}\sqrt{2})=\dfrac{ 1 +\dfrac{3}{2}\bigg(-1 -\dfrac{1}{2}\sqrt{2}\bigg)+1\bigg(-1 -\dfrac{1}{2}\sqrt{2}\bigg)^{2} }{ 1+1\bigg(-1 -\dfrac{1}{2}\sqrt{2}\bigg) }$ $= -\dfrac{1}{2}-1\sqrt{2}\approx-1.9142135623731$
$f(-1 +\dfrac{1}{2}\sqrt{2})=\dfrac{1 +\dfrac{3}{2}\bigg(-1 +\dfrac{1}{2}\sqrt{2}\bigg)+1\bigg(-1 +\dfrac{1}{2}\sqrt{2}\bigg)^{2} }{1+1\bigg(-1 +\dfrac{1}{2}\sqrt{2}\bigg) }$ $= -\dfrac{1}{2}+1\sqrt{2}\approx0.9142135623731$
Courbe représentative de f.
Proposition.
Soit $f$ une fonction dérivable et monotone sur un intervalle $I$ de $\mathbb{R}$.Exemple:Variations et signe de $f'(x)$.

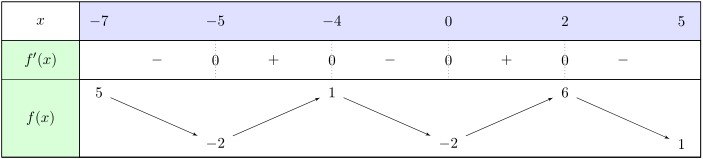
Par lecture graphique on peut lire que:
Définition.
Soit $f$ une fonction définie sur un intervalle $I$ de $\mathbb{R}$ et $a$ un réel appartenant à $I$.
On dit que $f$ admet un extremun local lorsqu'il existe un intervalle ouvert $J$ contenant $a$ inclus dans $I$ sur lequel $f(a)$ est un extremun de $f$. C'est à dire,
Théorème (admis en première).
Exemple.
Soit $ABCD$ un carré de coté 1. $M$ est un point du segment $[AB]$.
Sur la demi-droite portée par $(BC)$ d'origine $C$ ne contenant pas $B$, on place le point $N$ tel que $CN=AM$; la droite $(MN)$ coupe $(DC)$ en $P$.
On pose $AM=x$ avec $0\leq x\leq 1$.
Le but de l'exercice est de trouver la position de $M$ sur $[AB]$ pour que la distance $PC$ soit maximale.
