Nombre dérivé, tangente à la courbe d'une fonction.
Découverte du nombre dérivée
- Calculer la vitesse moyenne du trajet.
- Calculer la vitesse moyenne du trajet entre 3h et 5h de route.
- Sur quels intervalles de temps la vitesse semble-t-elle la moins rapide.
- A l'aide de la feuille Geogebra plus bas, évaluer la vitesse du véhicule exactement à l'instant $t=3h$.
- Conclure: qui a raison?
Nombre dérivé.
Exemples de calculs de nombres dérivés.
- Methode 1°: Pour $h\not=0$ on a:
$\dfrac{f(1+h)-f(1)}{h}=\dfrac{(1+h)^2-4}{h}$ $=\dfrac{(1+h)^2-2^2}{h}=\dfrac{(h+4)h}{h}$ $=\dfrac{f(1+h)-f(1)}{h}=h+4$. Quand $h$ tend vers 0 alors $h+4$ tend vers 4. On a donc $\displaystyle\lim_{h\to 0}(h+4)=4$.
Donc, $f^{'}(1)=\displaystyle\lim_{h\to 0}\frac{f(1+h)-f(1)}{h}=4$. - Methode 2°: Pour $x\not=1$ on a:
$\dfrac{f(x)-f(1)}{x-1}=\dfrac{(x+1)^2-4}{x-1}$ $=\dfrac{(x+1)^2-2^2}{x-1}=\dfrac{(x+3)(x-1)}{x-1}$ $\dfrac{f(x)-f(1)}{x-1}=x+3$. Quand $x$ tend vers 1 alors $x+3$ tend vers 4. On a donc $\displaystyle\lim_{x\to 3}(x+3)=4$.
Donc, $f^{'}(1)=\displaystyle\lim_{x\to 1}\frac{f(x)-f(1)}{x-1}=4$. - Calculer le nombre dérivé $f'(1)$.
- Donner le coefficient directeur de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}_f$ au point $A$ d'absicisse $2$.
- Calculons le quotient $\dfrac{f(1+h)-f(1)}{h}$ pour tout $h\not=0$.
$\dfrac{f(1+h)-f(1)}{h}=\dfrac{[4-(1+h)^2]-[4-1^2]}{h}$ $=\dfrac{1-(1+h)^2}{h}=\dfrac{-2h-h^2}{h}$ $=\dfrac{h(-2-2h)}{h}=-2-2h$.
Faisons tendre le réel $h$ vers $0$, quand $h\to 0$ alors $-2-2h\to -2$. On écrit cela mathématiquement $\displaystyle\lim_{h\to 0}(-2-2h)=-2$.
Donc $\displaystyle\lim_{h\to 0}\dfrac{f(1+h)-f(1)}{h}=-2$, donc $f$ est dérivable en 1 et le nombre dérivé $f'(1)$ existe et vaut -2; $f'(1)=-2$. - Le coefficient directeur de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}_f$ au point $A$ d'absicisse $2$, si il existe est égal au nombre dérivé $f'(2)$.
Calculons le quotient $\dfrac{f(2+h)-f(2)}{h}$ pour tout $h\not=0$.
$\dfrac{f(2+h)-f(2)}{h}=\dfrac{[4-(2+h)^2]-[4-2^2]}{h}$ $=\dfrac{4-(2+h)^2}{h}=\dfrac{-4h-h^2}{h}$ $=\dfrac{h(-4-2h)}{h}=-4-2h$.
Faisons tendre le réel $h$ vers $0$, quand $h\to 0$ alors $-4-2h\to -2$. On écrit cela mathématiquement $\displaystyle\lim_{h\to 0}(-4-2h)=-4$.
Donc $\displaystyle\lim_{h\to 0}\dfrac{f(2+h)-f(2)}{h}=-4$, donc $f$ est dérivable en 2 et le nombre dérivé $f'(2)$ existe et vaut -4; $f'(2)=-4$. Exemples de fonctions non dérivables.
- Si $h\geq 0$, alors $2+h\geq 2$ et donc $f(2+h)=-1$, donc $\dfrac{f(2+h)-f(2)}{h}=\dfrac{(-1)-(-1)}{h}=0$.
Donc quand $h$ tend vers $0$ tout en restant positif la fraction $\dfrac{f(2+h)-f(2)}{h}$ reste égale à zéro. On écrit cela mathématiquement:
$\displaystyle\lim_{h\to 0+}\dfrac{f(2+h)-f(2)}{h}=0$. - Si $h < 0$, alors $2+h < 2$ et donc $f(2+h)=1$, donc $\dfrac{f(2+h)-f(2)}{h}=\dfrac{1-(-1)}{h}=\dfrac{2}{h}$.
Donc quand $h$ tend vers $0$ tout en restant strictement négatif ($h\not=0$) la fraction $\dfrac{f(2+h)-f(2)}{h}=\dfrac{2}{h}$ devient trés grande en valeur absolue et négative. On écrit cela mathématiquement:
$\displaystyle\lim_{h\to 0-}\dfrac{f(2+h)-f(2)}{h}=-\infty$.
Interprétation graphique de $\displaystyle\lim_{h\to 0-}\dfrac{f(2+h)-f(2)}{h}=-\infty$.
La sécante $AM$ avec $A(2;-1)$ et $M(2+h,1)$, $h < 0$, devient verticale quand $h$ $h$ tend vers $0$ tout en restant strictement négatif ($h\not=0$). Le nombre dérivé ne peut donc pas exister puisque c'est un nombre par définition.
Voir animation ci-contre. Tangente à la courbe d'une fonction dérivable.
- Calculons le nombre dérivé $f'(2)$ qui donnera le coefficient directeur de la tangente $\mathcal{T}_A$.
Pour tout $h\not=0$ on a $\dfrac{f(2+h)-f(2)}{h}=\dfrac{0.5(2+h)^2-0.5\times 2^2}{h}$ $=\dfrac{0.5(4+4h+h^2)-2}{h}$ $=\dfrac{2h+0.5h^2}{h}=2+\dfrac{1}{2}h$.
Faisons tendre le réel $h$ vers $0$, quand $h\to 0$ alors $2+\dfrac{1}{2}h\to 2$. On écrit cela mathématiquement $\displaystyle\lim_{h\to 0}(2+\dfrac{1}{2}h)=2$.
Donc $\displaystyle\lim_{h\to 0}\dfrac{f(2+h)-f(2)}{h}=2$, donc $f$ est dérivable en 2 et le nombre dérivé $f'(2)$ existe et vaut 2; $f'(2)=2$.
D'aprés la propriété nous savons que $\mathcal{T}_A$, la tangente à $\mathcal{C}_f$ au point $A$ d'abscisse $2$, a pour équation réduite:
$y=f^{'}(x_0)(x-x_0)+f(x_0)$ $\Leftrightarrow$ $y=2(x-2)+2=2x-2$.
Donc ($\mathcal{T}_A):y=2x-2$. - Tracons $(\mathcal{T}_A):y=2x-2$.
- Ordonnée à l'origine=-2, Placer le point de coordonnées $(0;-2)$.
- Coefficient directeur =2.
- Donner l'équation de $\mathcal{T}_A$ la tangente à $\mathcal{C}_f$ au point $A$ d'abscisse 2.
- Tracer $\mathcal{T}_A$.
Activité: vitesse moyenne, vitesse instantanée.
On part pour un long trajet d'un peu plus de 600km. La courbe ci-dessous représente la distance parcourue f(x) (en km) en fonction du temps de trajet x (en heure). Les gendarmes nous ont arrêtés à la fin de notre parcours et nous ont accusé d'avoir fait un excès de vitesse. Impossible!! avons nous répondu. Qui a raison?
A l'aide de la feuille dynamique Géogebra répondez au questions suivantes:
Définition.
Soit $\mathcal{C}_f$ la courbe représentative d'une fonction $f$ dans un repère orthonormé $(O,\vec{i},\vec{j})$ du plan.
Soit $M_0$ un point de $\mathcal{C}_f$ d'abscisse $x_0$ et $M$ un point de $\mathcal{C}_f$ d'abscisse $x$ avec $x_0\not=x$.
La droite $(M_0M)$ est appelée une sécante à la courbe $\mathcal{C}_f$.
Proposition.
Le coefficient directeur de la sécante $(M_0M)$ est égal à: $\dfrac{f(x)-f(x_0)}{x-x_0}$ pour tout $x\not=x_0$.

Soit $\mathcal{C}_f$ la courbe représentative d'une fonction $f$ dans un repère orthonormé $(O,\vec{i},\vec{j})$ du plan.
Soit $M_0$ un point de $\mathcal{C}_f$ d'abscisse $x_0$ et $M$ un point de $\mathcal{C}_f$ d'abscisse $x$ avec $x_0\not=x$.
On a $y_{M_0}=f(x_{M_0})=f(x_0)$ et $y_M=f(x_M)=f(x)$. NOus savons que le coéfficient directeur de la droite $(M_0M)$ est égal à:
$a=\dfrac{y_{M}-y_{M_0}}{x_M-x_{M_0}}=$ $\dfrac{f(x)-f(x_0)}{x-x_0}$
pour tout $x\not=x_0$.
Définition.
Soit $f$ une fonction définie sur un intervalle $I$ de $\mathbb{R}$ et $x_0\in I$.
Lorsque le rapport $\displaystyle\frac{f(x)-f(x_0)}{x-x_0}$ admet une limite réelle quand $x$ tend vers $x_0$ en restant dans $I$,
on dit que la fonction $f$ est dérivable en $x_0$ et cette limite réelle , notée $f^{'}(x_0)$, est appelée le nombre dérivé de $f$ en $x_0$.
On a donc alors:
$\displaystyle\lim_{x\to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}=f^{'}(x_0)$.
Proposition.
Soit $f$ une fonction définie sur $I$ avec $x_0\in I$, $f$ est dérivable en $x_0$ alors le rapport $\displaystyle\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}$ admet une limite réelle quand $h$ tend vers 0 avec $x_0+h$ restant dans $I$.
Nous avons:
$\displaystyle\lim_{h\to 0}\dfrac{f(x_0+h)-f(x_0)}{h}=\displaystyle\lim_{x\to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}=f^{'}(x_0).$

Savoir tracer une courbe ayant des contraintes de points et de dérivée.
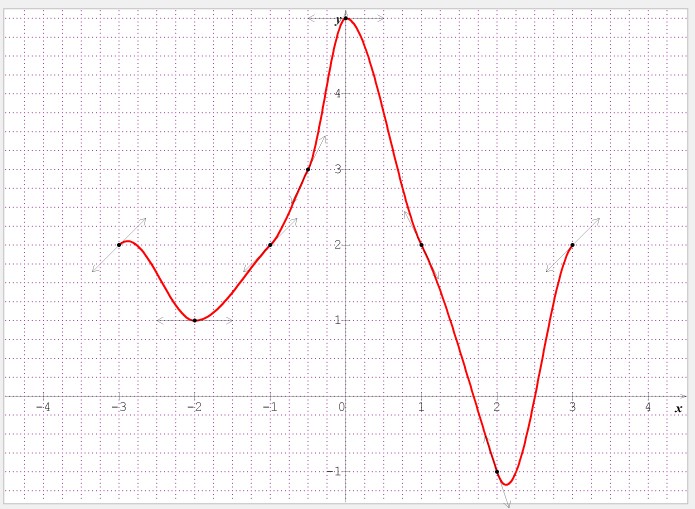
Dans un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$, tracer une courbe possible vérifiant les contraintes suivantes. Vous prendrez soin de tracer aussi les tangentes à cette courbe!
| N° de points | x | y | f'(x) |
| 1 | -3 | 2 | 1 |
| 2 | -2 | 1 | 0 |
| 3 | -1 | 2 | 1 |
| 4 | -0.5 | 3 | 2 |
| 5 | 0 | 5 | 0 |
| 6 | 1 | 2 | -2 |
| 7 | 2 | -1 | -3 |
| 8 | 3 | 2 | 1 |

Exemple.
Vérifions que $f$ définie sur $\mathbb{R}$ par $f(x)=(1+x)^2$ est dérivable en 1, calculer $f^{'}(1)$.Exercice.
Soit $f$ la fonction définie $\mathbb{R}$ par $f(x)=4-x^2$.
Dérivabilité de la fonction $x\mapsto|x|$.
Considérons la fonction valeur absolue, voici la représentation graphique, montrons que $x\mapsto|x|$ n'est pas dérivable en 0.
$\dfrac{|0+h|-|0|}{h}=\dfrac{|h|}{h}=\Bigg\{
\begin{array}[pos]{c}
\dfrac{h}{h}=1~~~~~~si~~~~h>0\\
\dfrac{-h}{h}=-1~~~~~~si~~~~h < 0\\
\end{array}.$
Donc nous avons simultanément $\displaystyle\lim_{h\to 0^+}\dfrac{|h|}{h}=1$ et $\displaystyle\lim_{h\to 0^-}\dfrac{|h|}{h}=-1$.
Donc la limite du rapport $\dfrac{|h|}{h}$ n'existe pas en $0$. Donc la fonction valeur absolue n'est pas dérivable en $0$.

Montrons que $f$ n'est pas dérivable en 2.
Le problème est que l'expression de $f(2+h)$ est fonction du signe de $h$, en effet:

Définition.
Soit une fonction $f$ dérivable en $x_0$, et soit $\mathcal{C}_f$ la courbe représentative de $f$.
La tangente à $\mathcal{C}_f$ au point $A(x_0;f(x_0))$ est la droite qui passe par $A$ et dont le coefficient directeur est $f^{'}(x_0)$.
Théorème.
Soit une fonction $f$ dérivable en $x_0$, et soit $\mathcal{C}_f$ la courbe représentative de $f$.
l'équation réduite de la tangente à $\mathcal{C}_f$ au point $A(x_0;f(x_0))$ est: $y=f^{'}(x_0)(x-x_0)+f(x_0)$.
$a=f'(x_0)$, puisque le nombre $a$ est le coefficient directeur de la droite $\mathcal{T}$. Le point $A$ appartient à $\mathcal{T}$, donc comme $A$ a pour coordonnées $(x_0,f(x_0))$, on a:
$f(x_0)=ax_0+b$ $\Leftrightarrow$ $f(x_0)=f'(x_0)\times x_0+b$ $\Leftrightarrow$ $b=f(x_0)-f'(x_0)\times x_0$.
Donc la droite $\mathcal{T}$ a pour équation réduite:
$y=f'(x_0)x+(f(x_0)-f'(x_0)\times x_0)=f^{'}(x_0)(x-x_0)+f(x_0)$


Exercice.
Soit la fonction $x\to\dfrac{1}{2}x^2$.