Variables aléatoires.
Rappel de probabilité.
- L'ensemble des issues d'une expérience aléatoire est appelé univers. En général on le note $\Omega$, et les issues sont les éléments de l'ensemble $\Omega$,
on les note souvent $e_1$, $e_2$,..., $e_n$.
$\Omega=\{e_1;e_2;...;e_n\}$. - Un événement est une sous-ensemble de $\Omega$. Un événement elémentaire est un événement qui ne contient qu'un seul élément de $\omega$.
- L'événement "A et B" correspond au sous-ensemble $A\cap B$ de $\Omega$.
- L'événement "A ou B" correspond au sous-ensemble $A\cup B$ de $\Omega$.
- L'événement "contraire de A" correspond au sous-ensemble $\overline{A}$ de $\Omega$.
- Deux événements sont incompatibles si $A\cap B=\emptyset$.
- Soit $\Omega=\{e_1;e_2;...;e_n\}$ un univers.
Définir une loi de probabilité $p$ sur $\Omega$, c'est associer à chaque événement élémentaire $e_i$ un nombre $p_i=p(e_i)$ tels que :
$0\leq p_i\leq 1$ et $p_1+p_2+...+p_n=1$.
Chaque nombre réel $p_i$ est appelé probabilité de l'événement $e_i$. - Une loi de probabilité est équirépartie si $p_1=p_2=...=p_n=\dfrac{1}{n}$.
Calculs de probabilité.
- Soit un univers $\Omega$ muni d'une loi de probabilité $p$.
La probabilité d'un événement $A$ que l'on note $P(A)$ est la somme des probabilités de tous les événements élémentaires inclus dans $A$. - Deux événements $A$ et $B$ sont équiprobables si $P(A)=P(B)$.
- Si $A\cap B=\emptyset$ alors $P(A\cup B)=P(A)+P(B)$.
- Si $A\cap B\not=\emptyset$ alors $P(A\cup B)=P(A)+P(B)-P(A\cap B)$.}
- $P(\overline{A})=1-P(A)$.
- Supposons que $A\cap B=\emptyset$, donc $A$ et $B$ n'ont aucun événement élémentaire commun.
$P(A\cup B)=\sum_{e\in A\cup B}P(\{e\})=\sum_{e\in A}P(\{e\})+\sum_{e\in B}P(\{e\})=P(A)+P(B)$. - Cas général, si $A\cap B\not=\emptyset$.
Nous savons que $P(A\cup B)=\sum_{e\in A\cup B}P(\{e\})$. Quand on éffectue la somme $\sum_{e\in A}P(\{e\})+\sum_{e\in B}P(\{e\})$, tous les nombres $P(\{e\})$ avec $e\in A\cap B$ vont être compter deux fois.
Donc $P(A\cup B)=P(A)+P(B)-P(A\cap B)$. - On remarque que $\Omega=A\cup \bar{A}$ et $A\cap\bar{A}=\emptyset$.
Donc d'après la premiére relation on a: $1=P(\Omega)=P(A)+P(\bar{A})$.
Donc $P(\overline{A})=1-P(A)$. Variables aléatoires.
- Quelles sont les valeurs prises par $X$?
- Déterminer la loi de probabilité de la variable aléatoire $X$.
- En déduire $P(X\leq 3)$ et $P(X>3)$.
- L'ensemble des issues de cet univers est $\Omega=\{(p;p);(p,f);(f;f);(f;p)\}$.
- Si on obtient deux piles, on gagne 10 euros.
- Si on obtient (p;f) ou (f;p), on gagne 3 euros.
- Si on obtient deux faces, on perd 4 euros.
- Calculons la loi de probabilité de $X$. On a:
$k$ $-4$ $3$ $10$ $P(X=k)$ $\dfrac{1}{4}$ $\dfrac{1}{2}$ $\dfrac{1}{4}$ - $P(X\leq 3)=P(X=-4)+P(X=3)=\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{3}{4}$.
$P(X>3)=P(\overline{X\leq 3})=1-P(X\leq 3)=1-\dfrac{3}{4}=\dfrac{1}{4}$. Espérance, variance, écart type d'un variable aléatoire.
- L'espérance Mathématique de $X$ est le nombre réel, noté $E(X)$ et $E(X)=x_1\times p(X=x_1)+x_2\times P(X=x_2)+...+x_m\times p(X=x_m)$.
- La variance de $X$ est le nombre réel, noté $V(X)$ et $V(X)=(x_1-E(X))^2\times p(X=x_1)+(x_2-E(X))^2\times p(X=x_2)+...+(x_m-E(X))^2\times p(X=x_m)$.
- L'écart type de $X$ est le nombre réel, noté $\sigma(X)$ et $\sigma(X)=\sqrt{V(X)}$.
- deux points si le nombre est pair
- trois points si le nombre obtenu est premier,
- cinq points obtenu est un multiple de 5,
- sept points, si le nombre est un carré parfait. Les point sont cumulables. Soit la variable aléatoire $X$ qui associe au lancer du dé le nombre de points marqués par le joueur.
- Déterminer la loi de probabilité de $X$
- En déduire $P(X\leq 5)$, $P(3\leq X\leq 7)$ et $P(X>7)$.
- Calculer $E(X)$ et $V(X)$.
- La variable $X$, prend exclusivement les valeurs -7; 2; 3;5. On écrit cela par $Im(X)=\bigg\{2;3;5;7;8;9\bigg\}$.
- $P(X=2)=P(\{6;8;12;14;18\}$ $=\dfrac{5}{20}=\dfrac{1}{4}$.
- $P(X=3)=P(\{3;7;11;13;17;19\})$ $=\dfrac{6}{20}=\dfrac{3}{10}$.
- $P(X=5)=P(\{2;15\})=\dfrac{2}{20}=\dfrac{1}{10}$.
- $P(X=7)=P(\{1;9;10;20\})=\dfrac{4}{20}=\dfrac{1}{5}$.
- $P(X=8)=P(\{8\})=\dfrac{1}{20}$.
- $P(X=9)=P(\{4;16\})=\dfrac{2}{20}=\dfrac{1}{10}$.
$k$ 2 3 5 7 8 9 $P(X=k)$ $\dfrac{5}{20}$ $\dfrac{6}{20}$ $\dfrac{2}{20}$ $\dfrac{4}{20}$ $\dfrac{1}{20}$ $\dfrac{2}{20}$ 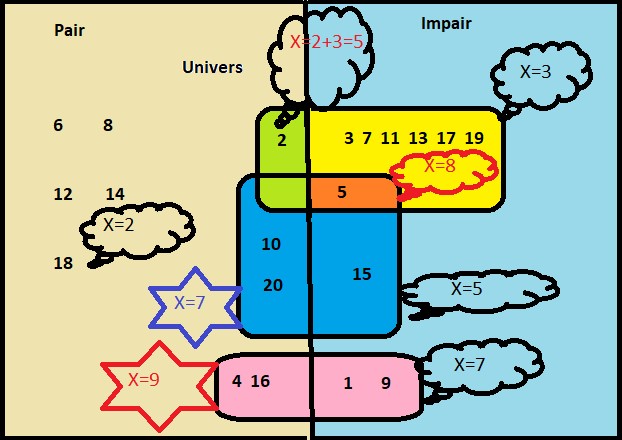
-
- $P(X\leq 5)=P(X=2)+P(X=3)+P(X=5)$ $=\dfrac{5}{20}+\dfrac{6}{20}+\dfrac{2}{20}=\dfrac{13}{20}$.
- $P(3\leq X\leq 7)=P(X=3)+P(X=5)+P(X=7)$ $=\dfrac{6}{20}+\dfrac{2}{20}+\dfrac{4}{20}=\dfrac{12}{20}=\dfrac{3}{5}$.
- $P(X>7)=P(X=8)+P(X=9)$ $=\dfrac{1}{20}+\dfrac{2}{20}=\dfrac{3}{20}$.
- $E(X)=2\times P(X=2)+3\times P(X=3)+5\times P(X=5)+7\times P(X=7)+8\times P(X=8)+9\times P(X=9)=\dfrac{92}{20}$
- $V(X)=E(X^2)-(E(X))^2$ $=2^2\times P(X=2)+3^2\times P(X=3)+5^2\times P(X=5)+7^2\times P(X=7)+8^2\times P(X=8)+9^2\times P(X=9)-\bigg(\dfrac{92}{20}\bigg)^2$.
- $V(X)=(x_1-E(X))^2\times p(X=x_1)+(x_2-E(X))^2\times p(X=x_2)+...+(x_m-E(X))^2\times p(X=x_m)$
$=\sum_{j=1}^{n} (x_j-E(X))^2\times P(X=x_j)$ $=\sum_{j=1}^{n} (x_j^2-2x_jE(X)+E(X)^2)\times P(X=x_j)$
$=\sum_{j=1}^{n} (x_j^2-2x_jE(X)+E(X)^2)\times P(X=x_j)$
$=\sum_{j=1}^{n} x_j^2\times P(X=x_j)-2E(X)\times\bigg(\sum_{j=1}^{n} x_j\times P(X=x_j)\bigg)+E(X)^2\times\bigg(\sum_{j=1}^{n} P(X=x_j)\bigg)$.
Or on sait que, $\sum_{j=1}^{n} P(X=x_j)=1$, donc nous avons:
$V(X)=\sum_{j=1}^{n} x_j^2\times P(X=x_j)-2E(X)\times E(X)+E(X)^2$ $=\sum_{j=1}^{n} x_j^2\times P(X=x_j)-E(X)^2$. - Le nombre $\sum_{j=1}^{n} x_j^2\times P(X=x_j)$ représente l'espérance mathématiques de la variables aléatoires $X^2$.
Nous pouvons donc écrire $\sum_{j=1}^{n} x_j^2\times P(X=x_j)=E(X^2)$. donc nous avons $V(X)=E(X^2)-(E(X))^2$. Espérance de aX+b et variance de aX.
- Notons $x_1$;...;$x_n$, les valeurs prises par la variables aléatoire $X$, alors $aX+b$ prend les valeurs $ax_1+b$; $ax_2+b$;...; $ax_n+b$.
Nous avons $E(aX+b)=\sum_{j=1}^n (ax_j+b)\times P(aX=ax_j)$.
Or $aX+b=ax_i+b$ $\Leftrightarrow$ $X=x_i$ pour tout $i\in\{1;...;n\}$, donc nous avons $P(aX+b=ax_j+b)=P(X=x_j)$.
Donc nous avons $E(aX+b)=\sum_{j=1}^n (ax_j+b)\times P(aX+b=ax_j+b)$ $=a\times\bigg(\sum_{j=1}^n x_j\times P(X=x_j)\bigg)+b\times\bigg(\sum_{j=1}^n P(X=x_j)\bigg)$ $=a\times E(X)+b$. - Notons $x_1$;...;$x_n$, les valeurs prises par la variables aléatoire $X$, alors $aX$ prend les valeurs $ax_1$; $ax_2$;...; $ax_n$ et nous savons que
$P(aX=ax_j)=P(X=x_j)$.
$V(aX)=\sum_{j=1}^n (ax_j-E(aX))^2\times p(aX=ax_j)$ $=\sum_{j=1}^n [a(x_j-E(X))]^2\times p(X=x_j)$ $=\sum_{j=1}^n a^2(x_j-E(X))^2\times p(X=x_j)$ $=a^2\times\bigg(\sum_{j=1}^n (x_j-E(X))^2\times p(X=x_j)\bigg)$ $=a^2V(X)$. - $E(aX+b)=aE(X)+b$.
- $V(aX)=a^2V(X)$
Définitions.

Loi de probabilité.
Définition.
Notation: soit $E$ un ensemble fini, on note $Card(E)$ le nombre d'éléments contenus dans $E$.
Propriété.
Soit $\Omega$ un univers de cardinal fini muni d'une loi équirépartie $p$, et soit $A$ un événement de $\Omega$, alors on a:
$P(A)=\dfrac{Card(A)}{Card(\Omega)}=\dfrac{nombre~~d'elements~~de~~A}{nombre~~d'elements~~de~~\Omega}$.
On a en particulier,
$P(\Omega)=1$ et $P(\emptyset)=0$.
Théorème.
Soit $\Omega$ un univers muni d'une loi de probabilité $p$, et soit $A$ et $B$ deux événements de $\Omega$, alors on a:

Soit $\Omega$ un univers muni d'une loi de probabilité $p$, et soit $A$ et $B$ deux événements de $\Omega$.
Définition.
Soit $\Omega$ un univers, toute fonction $X$ définie sur $\Omega$ et à valeur dans $\mathbb{R}$, est appelée une variable aléatoire.
$X:\Omega\longmapsto\mathbb{R}$.
Exemple.
Lançons simultanément deux dés. Considérons La variable aléatoire $X$ qui donne la somme des nombres indiqués sur les deux dés.
On peut utiliser un algorithme pour simuler cette petite expérience aléatoire.
Ici $X$ prend les valeurs $\{2;3;4;5;6;7;8;9;10;11;12\}$.
La fonction python randint(1,6) permet de simuler un dé.

Loi de probabilité d'une variable aléatoire.
Soit $X$ une variable aléatoire définie sur l'univers $\Omega$, Notons $I$ l'ensemble des valeurs de $X$, $I=\{x_1;x_2;...;x_m\}$.
Considérons l'événement "X prend la valeur $x_i$", que l'on note $(X=x_i)$.
A chaque événement $(X=x_i)$ on associe le nombre $p(X=x_i)$, c'est à dire la probabilité que $X$ prenne la valeur $x_i$.
La loi de probabilité de $X$ est la suite des nombres:
$p(X=x_1);p(X=x_2);...,p(X=x_m)\}$.
Exemple
Un jeu consiste à lancer deux fois de suites une pièces de monnaie. On gagne $5$ euros à chaque fois que la pièce tombe sur pile et on perd 2 euros chaque fois que la pièce tombe sur face.
On note $X$ la variable aléatoire qui, à chaque partie associe le gain.
Définitions.
Soit $X$ une variable aléatoire définie sur un univers $\Omega$.
Exemple.
Dans un jeu familial, on lance un dé icosaédrique, dont les faces sont numérotées de 1 à 20, que l'on suppose bien équilibré. On marque:
Propriété.
$V(X)=\Sigma_{i=1}^{i=n}\bigg(p_i\times x_i^2\bigg)-E(X)^2$. On peut aussi noter cela: $V(X)=E(X^2)-(E(X))^2$.Définition.
Soit $\Omega$ un univers et $X:\Omega\longmapsto\mathbb{R}.$ une variable aléatoire sur cet univers.
On note $aX+b$, avec $a\in\mathbb{R}$ et $b\in\mathbb{R}$, la variable aléatoire qui a chaque événement $\omega$ de $\Omega$ associe le réel $a\times X(\omega)+b$.
Proposition.
Soit $X$ une variable aléatoire sur un univers $\Omega$, pour tout $a\in\mathbb{R}$ et $b\in\mathbb{R}$ on a: