Suites numériques.
Définitions et généralités sur les suites numériques.
- Suites définies par la donnée explicite de leur termes.
Soit $ \begin{array}[]{ccc} f:\mathbb{R}&\longmapsto&\mathbb{R}\\ x&\longmapsto&f(x) \end{array}$ une fonction définie sur $\mathbb{R}$, posons $\forall n\in\mathbb{N}$ $u_n=f(n)$.
Remarque: L'avantage d'une suite explicite est de pouvoir calculer directement $u_{100}$ par exemple il suffira de calculer $u_{100}=f(100)$.Exemples de suites explicites
- $u_n=\dfrac{1}{n+1}$ pour tout $n\in\mathbb{N}$, par exemple $u_{100}=\dfrac{1}{101}$.
- $u_n=n^2-3n+1$ pour tout $n\in\mathbb{N}$, par exemple $u_{10}=10^2-3\times 10+1=71$.
- Suites définies par recurrence.
Soit un sous ensemble $I\subset\mathbb{R}$ et $\begin{array}[]{ccc} f:I&\longmapsto&\mathbb{R}\\ x&\longmapsto&f(x) \end{array}$ une fonction définie sur $I$ telle que $f(I)\subset I$ Posons $u_0=a\in I$ et $\forall n\in\mathbb{N}$ $u_{n+1}=f(u_n).$
Remarque: L'inconvénient d'une suite définie par récurrence est que l'on ne peurt pas calculer directement $u_{100}$. Il faudra calculer tous les termes de proche en proche jusqu'au rang $n=100$.
- $u_0=1$ et $u_{n+1}=\dfrac{u_n}{u_n+1}$ pour tout $n\in\mathbb{N}$.
- $v_0=3$ et $v_{n+1}=(v_n^2)-v_n$ pour tout $n\in\mathbb{N}$.
- $w_0=1$ et $w_{n+1}=2\times w_n+(n+1)$ pour tout $n\in\mathbb{N}$.
$w_1=2\times w_0+(0+1)=2+1=3$; $w_2=2\times w_1+(1+1)=2\times 3+2=8$; $w_3=2\times w_2+(2+1)=16+3=19$ etc.... Représentation d'une suite numérique.
- en plaçant les réls $u_0$, $u_1$, $u_2$, etc sur une droite graduée,
- soit en plaçant les points de coordonnées $(n,u_n)$ dans un repère.
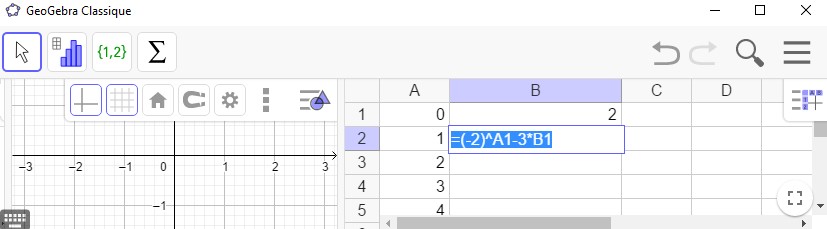
- Etape 1: On écrit dans cellule B2 =(-2)^A1-3*B1
- Etape 2: On sélectionne la cellule B2 et on glisse vers le bas:
Etude de la monotonie des suites réelles.
Définitions.
- Dire qu'une suite $(u_n)$ est croissante signifie que pour tout $n\in\mathbb{N}$, on a $u_n\leq u_{n+1}$.
- Dire qu'une suite $(u_n)$ est strictement croissante signifie que pour tout $n\in\mathbb{N}$, on a $u_n < u_{n+1}$.
- Dire qu'une suite $(u_n)$ est décroissante signifie que pour tout $n\in\mathbb{N}$, $u_n\geq u_{n+1}$.
- Dire qu'une suite $(u_n)$ est strictement décroissante signifie que pour tout $n\in\mathbb{N}$, $u_n>u_{n+1}$.
Différentes techniques pour étudier la montonie d'une suite.
- Méthode 1:Etudier le signe de la différence $u_{n+1}-u_n$.
- Si pour tout $n\in\mathbb{N}$, $u_{n+1}-u_n\geq 0$, alors la suite est croissante.
- Si pour tout $n\in\mathbb{N}$, $u_{n+1}-u_n\leq 0$, alors la suite est décroissante.
- Si pour tout $n\in\mathbb{N}$, $u_{n+1}-u_n>0$, alors la suite est strictement croissante.
- Si pour tout $n\in\mathbb{N}$, $u_{n+1}-u_n < 0$, alors la suite est strictement décroissante.
- Méthode 2:Si pour tout $n\in\mathbb{N}$, $u_n>0$}, on peut comparer le quotient $\frac{u_{n+1}}{u_n}$ avec le nombre $1$.
- Si pour tout $n\in\mathbb{N}$, $\frac{u_{n+1}}{u_n}\geq 1$, alors la suite est croissante.
- Si pour tout $n\in\mathbb{N}$, $\frac{u_{n+1}}{u_n}\leq 1$, alors la suite est décroissante.
- Si pour tout $n\in\mathbb{N}$, $\frac{u_{n+1}}{u_n}>1$, alors la suite est strictement croissante.
- Si pour tout $n\in\mathbb{N}$, $\frac{u_{n+1}}{u_n} < 1$, alors la suite est strictement décroissante.
- Methode 3: Etudier le sens de variation de la fonction $f$ telle que $u_{n}=f(n)$.
- Si la fonction est croissante sur $[0;+\infty[$, alors la suite $(u_n)$ est croissante.
- Si la fonction est décroissante sur $[0;+\infty[$, alors la suite $(u_n)$ est décroissante.
- Si la fonction est strictement croissante sur $[0;+\infty[$, alors la suite $(u_n)$ est strictement croissante.
- Si la fonction est strictement décroissante sur $[0;+\infty[$, alors la suite $(u_n)$ est strictement décroissante.
- Soit $(u_n)$ la suite définie pour tout entier naturel $n$ par $u_n=\dfrac{1}{n+2}$.
$u_{n+1}-u_n=\dfrac{1}{(n+1)+2}-\dfrac{1}{n+2}$ $=\dfrac{1}{n+3}-\dfrac{1}{n+2}$ $=\dfrac{(n+2)-(n+3)}{(n+2)(n+3)}=-\dfrac{1}{(n+2)(n+3)}$
Le nombre $(n+2)(n+3)>0$ pour tout $n\in\mathbb{N}$, donc $u_{n+1}-u_n < 0$, donc la suite $(u_n)$ est strictement décroissante. - Soit $(v_n)$ la suite définie pour tout entier naturel $n$ par $v_n=n^2+2n$.
$v_{n+1}-v_n=(n+1)^2+2(n+1)-(n^2+2n)$ $=2n+3$
Le nombre $(2n+3)>0$ pour tout $n\in\mathbb{N}$, donc $v_{n+1}-v_n > 0$, donc la suite $(v_n)$ est strictement croissante.
- Soit $u_n=\dfrac{2^{n+1}}{3^n}$ pour tout $n\in\mathbb{N}$.
Il est clair que $u_n>0$ pour tout $n\in\mathbb{N}$,
$\dfrac{u_{n+1}}{u_n}=\dfrac{\dfrac{2^{(n+1)+1}}{3^{n+1}}}{\dfrac{2^{n+1}}{3^n}}$ $=\dfrac{\dfrac{2^{(n+1)}\times 2}{3^{n}\times 3}}{\dfrac{2^{n+1}}{3^n}}$ $=\dfrac{2^{(n+1)}\times 2}{3^{n}\times 3}\times\dfrac{3^n}{2^{n+1}}$ $=\dfrac{2}{3} < 1$, donc $\dfrac{u_{n+1}}{u_n} < 1$ et $u_n>0$ pour tout $n\in\mathbb{N}$.
Donc la suite (u_n) est strictement décroissante. - Soit $v_n=\dfrac{2^{2n}}{3^n}$ pour tout $n\in\mathbb{N}$.
Il est clair que $v_n>0$ pour tout $n\in\mathbb{N}$,
$\dfrac{v_{n+1}}{v_n}=\dfrac{\dfrac{2^{2(n+1)}}{3^{n+1}}}{\dfrac{2^{n+1}}{3^n}}$ $=\dfrac{\dfrac{2^{(2n+2)}}{3^{n}\times 3}}{\dfrac{2^{2n}}{3^n}}$ $=\dfrac{\dfrac{2^{2n}\times 2^2}{3^{n}\times 3}}{\dfrac{2^{2n}}{3^n}}$ $=\dfrac{2^{2n}\times 4}{3^{n}\times 3}\times\dfrac{3^n}{2^{2n}}$ $=\dfrac{4}{3}> 1$, donc $\dfrac{v_{n+1}}{v_n}> 1$ et $v_n>0$ pour tout $n\in\mathbb{N}$.
Donc la suite $(u_n)$ est strictement croissante.
- Soit la suite $(u_n)$ définie pour tout $n\geq1$ et $u_n=n^4-\dfrac{4}{3}n^3$.
On peut remarquer que $u_n=f(n)$ avec la fonction $f$ définie par $(f(x)=x^4-\dfrac{4}{3}x^3$; Etudions les variation de $f$ sur l'intervalle $[1;+\infty[$.
$f'(x)=4x^3-\dfrac{4}{3}\times 3x^2=4x^3-4x^2=x^2(x-1)$. Etudions le signe de $f'(x)$, $x\in[1;+\infty[$ donc $x\geq 1$ donc $x-1\geq 0$.
Donc $f'(x)\geq 0$, la fonction $f$ est croissante sur $[1;+\infty[$, donc la suite $(u_n)$ est croissante.
les suites arithmétiques.
- Dire qu'une suite $(u_n)$ est arithmétique signifie qu'il existe un réel r tel que pour tout naturel $n\in\mathbb{N}$, on a $u_{n+1}=u_n+r$.
Le réel $q$ est appelé la raison de la suite $(u_n)$. - Soit $(u_n)$ une suite arithmétique de premier terme $u_0$ et de raison $r$, alors pour tout entier $n$, on a $u_n=u_0+nr$.
- Soit $(u_n)$ une suite arithmétique de premier terme $u_0$ et de raison $r$, alors pour tout entier $n$ et $p$, on a $u_n=u_p+(n-p)r$.
- Une suite arithmétique de raison $r$ est:
- strictement croissante si $r>0$;
- strictement décroissante si $r < 0$;
- constante si $r=0$
- La relation $u_n=u_0+nr$ est un cas particulier de la relation $u_n=u_p+(n-p)r$ avec $p=0$, prouvons donc cette relation plus générale.
- Prouvons que pour tout $n\in\mathbb{N}$, et $p\in\mathbb{N}$, on a $u_n=u_p+(n-p)r$.
- Premier cas; si $0\leq p\leq n$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à additionner $(n-p)$ fois la raison $r$ au nombre $u_p$.
Autrement dit $u_n=u_p+(n-p)r$. - Deuxième cas; si $0\leq n\leq p$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à soustraire $(p-n)$ fois la raison $r$ au nombre $u_p$.
Autrement dit $u_n=u_p-(p-n)r$, donc $u_n=u_p+(n-p)r$.
- Premier cas; si $0\leq p\leq n$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à additionner $(n-p)$ fois la raison $r$ au nombre $u_p$.
- Soit une suite (u_n) arithmétique de raison $r$. Pour tout $n\in\mathbb{N}$, on a:
$u_{n+1}-u_n=(u_n+r)-u_n=r$, donc:- strictement croissante si $r>0$;
- strictement décroissante si $r < 0$;
- constante si $r=0$
- Soit $(u_n)$ une suite arithmétique, dans chaque cas déterminer $u_{20}$.
- La raison est $r=3$ et $u_7=12$.
- La raison est $r=5$ et $u_{25}=17$.
- Soit $(u_n)$ une suite arithmétique de premier terme $u_0=-10$ et de raison $\dfrac{1}{3}$, le nombre $\dfrac{794}{3}$ fait-il partie de la suite $(u_n)$?
- Soit $(u_n)$ une suite arithmétique de premier terme $u_0=-1$ et telle que sont 100 ième terme est égal à 1000, quelle est la raison de cette suite suite?
- $u_{20}=u_7+(20-7)\times r=12+13\times 3=51$.
- $u_{25}=u_{20}+(25-20)\times r$, donc $17=u_{20}+5\times 5$, donc $u_{20}=17-25=-8$.
- Déterminons si il existe un entier naturel $n$, pour que $u_n=\dfrac{794}{3}$. Or $(u_n)$ est une suite arithmétique de premier terme $u_0=-10$ et de raison $\dfrac{1}{3}$.
Donc $u_n=u_0+n\times \dfrac{1}{3}=-10+\dfrac{n}{3}=\dfrac{n-30}{3}=\dfrac{794}{3}$.
$\dfrac{n-30}{3}=\dfrac{794}{3}$ $\Leftrightarrow$ $n-30=794$ $\Leftrightarrow$ $n=824$.
$n=824$ est bien un entier naturel, cela correspond bien à un indice de suites. On a $u_{824}=\dfrac{794}{3}$. - Nous savons que 100 ième terme est égal à 1000, donc $u_{99}=1000$.
Donc $u_{99}=u_0+99\times r=1000$ $\Leftrightarrow$ $-1+99r=1000$ $\Leftrightarrow$ $99r=1001$ $\Leftrightarrow$ $r=\dfrac{1001}{99}$ - Cas particulier: $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$.
- Soit $(u_n)$ une suite arithmétique de raison $r$, alors on a $S_n=u_0+u_1+...+u_n$ $=\dfrac{n+1}{2}(u_0+u_n)=\dfrac{n+1}{2}(2u_0+n\times r)$.
- Montrons que $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$.
$S_n=1+2+...+(n-1)+n$
$S_n=n+(n-1)+...+2+1$
+------------------------------------------------
$2S_n=(1+n)+(2+n-1)+...+(n-2+1)+(n+1)$
$2S_n=(n+1)+(n+1)+...+(n+1)+(n+1)$.
Il y a n termes égaux à $(n+1)$ à additionner, donc $2S_n=n\times(n+1)$, donc $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$. - Montrons que $S_n=u_0+u_1+...+u_n=\frac{n+1}{2}(u_0+u_n)=\frac{n+1}{2}(2u_0+n\times r)$. Considérons $0\leq j\leq n$, on a:
$S_n=u_0+u_1+...+u_j+...+u_{n-1}+u_n$
$S_n=u_n+u_{n-1}+...+u_{n-j}+...+u_1+u_0$
+-----------------------------------------------------------
$2S_n=(u_0+u_n)+(u_1+u_{n-1})+...+(u_j+u_{n-j})+...+(u_{n-1}+u_1)+(u_n+u_0)$.
$u_0+u_n=u_0+u_0+nr=2u_0+nr$, $u_1+u_n=u_0+r+u_0+(n-1)r=2u_0+nr$, de même pour tout $0\leq j\leq n$, on a $u_j+u_{n-j}=u_0+jr+u_0+(n-j)r=2u_0+nr$.
Donc Il y a $n+1$ termes égaux à $u_0+u_n=2u_0+nr$ à additionner.
Donc $S_n=\dfrac{n+1}{2}(u_0+u_n)=\dfrac{n+1}{2}(2u_0+n\times r)$. - $S=1+2+3+...+73$.
- $S=71+72+...+100$.
- $S=1+4+7+...+142$.
- $S=1+2+3+...+73$, on applique la formule $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$, avec $n=73$.
Donc $S=\dfrac{73\times 74}{2}=2701$. - Pour calculer cette somme on peut procéder de deux façons:
- Première façon, comme l'écart entre les termes de la somme est de 1, on peut utiliser la formule $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$, en remarquant que:
$S=71+72+...+100=(70+1)+(70+2)+...+(70+30)$, il y a 30 termes dans cette somme et donc $S=30\times 70+(1+2+3+...+30)$.
Donc $S=30\times 70+\dfrac{30\times 31}{2}=2565$. - Deuxième façon, $S$ est la somme des termes d'une suite arithmétique $(u_n)$ de premier terme $u_0=71$ et de raison $r=1$, le terme général de $(u_n)$ est $u_n=71+n$.
On a $u_{29}=100$, donc en appliquant la formule $S_n=u_0+u_1+...+u_n=\dfrac{n+1}{2}(u_0+u_n)$, avec $n=29$, on obtient:
$S=\dfrac{30}{2}(71+100)=2565$.
- Première façon, comme l'écart entre les termes de la somme est de 1, on peut utiliser la formule $S_n=1+2+...+n=\dfrac{n(n+1)}{2}$, en remarquant que:
- $S$ est la somme des termes d'une suite arithmétique $(u_n)$ de premier terme $u_0=1$ et de raison $r=3$, le terme général de $(u_n)$ est $u_n=1+3n$.
Recherchons l'indice $n$, on a $1+3n=142$ $\Leftrightarrow$ $3n=141$ $\Leftrightarrow$ $n=47$. On a $u_{47}=141$, donc en appliquant la formule $S_n=u_0+u_1+...+u_n=\dfrac{n+1}{2}(u_0+u_n)$, avec $n=29$, on obtient:
$S=\dfrac{(47+1)}{2}(1+142)=3976$. Les suites géométriques.
- Dire qu'une suite $(u_n)$ est géométrique signifie qu'il existe un réel $q$ tel que pour tout $n\in\mathbb{N}$, on a $u_{n+1}=q\times u_n$.
Le réel $q$ est appelé la raison de la suite $(u_n)$. - Soit $(u_n)$ une suite géométrique de premier terme $u_0$ et de raison $q$, alors pour tout entier $n$, on a $u_n=u_0\times q^n$.
- Soit $(u_n)$ une suite géométrique de premier terme $u_0$ et de raison $q$, alors pour tout entier $n$ et $p$, on a $u_n=u_p \times q^{n-p}$.
- Une suite géométrique de raison $q$ tel que $u_0>0$ est:
- strictement croissante si $q>1$;
- strictement décroissante si $0 < q < 1$;
- constante si $q=1$
- La relation $u_n=u_0\times q^n$ est un cas particulier de la relation $u_n=u_p \times q^{n-p}$ avec $p=0$, prouvons donc cette relation plus générale.
- Prouvons que pour tout $n\in\mathbb{N}$, et $p\in\mathbb{N}$, on a $u_n=u_p \times q^{n-p}$.
- Premier cas; si $0\leq p\leq n$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à multiplier $(n-p)$ fois la raison $q$ au nombre $u_p$.
Autrement dit $u_n=u_p\times q^{(n-p)}$. - Deuxième cas; si $0\leq n\leq p$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à diviser $(p-n)$ fois la raison $q$ au nombre $u_p$.
Autrement dit $u_n=\dfrac{u_p}{q^{(p-n)}}$, donc $u_n=u_p\times q^{-(p-n)}=u_p\times q^{(n-p)}$.
- Premier cas; si $0\leq p\leq n$ pour calculer $u_n$ sachant que l'on connait $u_p$ revient à multiplier $(n-p)$ fois la raison $q$ au nombre $u_p$.
- Soit une suite (u_n) géométrique de raison $r$. Commme $u_n=u_0\times q^n$, $q>0$ et $u_0>0$, alors pour tout $n\in\mathbb{N}$ $u_n>0$.
On peut donc utiliser le critère de croissance $\dfrac{u_{n+1}}{u_n}$.
$\dfrac{u_{n+1}}{u_n}=\dfrac{q\times u_n}{u_n}=q$, donc la suite (u_n) est:- strictement croissante si $q>1$;
- strictement décroissante si $0 < q < 1$;
- constante si $q=1$
- Soit $(u_n)$ une suite géométrique, dans chaque cas déterminer $u_{20}$.
- La raison est $q=3$ et $u_{10}=12$.
- La raison est $q=-2$ et $u_{31}=32$.
- Soit $(u_n)$ une suite géométrique de premier terme $u_0=-10$ et de raison $2$, le nombre $-655360$ fait-il partie de la suite $(u_n)$?
- Soit $(u_n)$ une suite géométrique de premier terme $u_0=1$ et telle que sont 4 ième terme est égal à $343$, quelle est la raison de cette suite suite?
- $u_{20}=u_{10}\times q^{(20-10)}=12\times 3^{10}=708588$.
- $u_{20}=u_{31}\times q^{(20-31)}$, donc $u_{20}=32\times (-2)^{-11}=-2^{-6}=-\dfrac{1}{64}$.
- Déterminons si il existe un entier naturel $n$, pour que $u_n=-655360$. Or $(u_n)$ est une suite géométrique de premier terme $u_0=-10$ et de raison $2$.
Donc $u_n=u_0\times q^n=-10\times 2^n=-655360$.
$-10\times 2^n=-655360$ $\Leftrightarrow$ $2^n=65536$ $\Leftrightarrow$ $n=16$.
$n=16$ est bien un entier naturel, cela correspond bien à un indice de suites. On a $u_{16}=-655360$. - Nous savons que 4 ième terme est égal à 343, donc $u_{3}=343$.
Donc $u_{3}=u_0\times q^3=343$ $\Leftrightarrow$ $q^3=343$ $\Leftrightarrow$ $q=\sqrt[3]{343}=7$. - Cas particulier: $S_n=1+q+q^2+...+q^n=\dfrac{1-q^{n+1}}{1-q}$.
- Soit $(u_n)$ une suite géométrique de raison $q$, avec $q\not=1$, alors on a $S_n=u_0+u_1+...+u_n$ $=u_0\times\dfrac{1-q^{n+1}}{1-q}$.
- Montrons que $S_n=1+q+q^2+...+q^n=\dfrac{1-q^{n+1}}{1-q}$.
$S_n=1+q+q^2+...+q^{n-1}+q^n$
$q\times S_n=q+q^2+...+q^n+q^{n+1}$
(soustraction)------------------------------------------------
$S_n-q\times S_n=\bigg(1+q+q^2+...+q^{n-1}+q^n\bigg)-\bigg(q+q^2+...+q^n+q^{n+1}\bigg)$
$(1-q)S_n=1-q^{n+1}$.
Iy a de cas à considérer.- Donc si $q\not=1$ , on a $S_n=1+q+q^2+...+q^n=\dfrac{1-q^{n+1}}{1-q}$.
- Si q=1, la somme est évidente et on a $S_n=1+1+...+1=(n+1)$.
- Montrons que $S_n=u_0+u_1+...+u_n=u_0\times\dfrac{1-q^{n+1}}{1-q}$.
Nous savons que pour tout $0\leq j\leq n$, on a: $u_j=u_0\times q^j$ $S_n=u_0+u_0\times q+...+u_0\times q^j+...+u_0\times q^{n-j}+u_0\times q^n$
$S_n=u_0\times\bigg(1+q+q^2+...+q^n\bigg)$
$S_n=u_0\times\dfrac{1-q^{n+1}}{1-q}$ - $S=1+2+4+16+...+262144$.
- $S=3-6+12-24+...+192$.
- $S=9+3+1+\dfrac{1}{3}...+\dfrac{1}{729}$.
- $S=1+2+4+16+...+262144$, on applique la formule $S_n=1+q+q^2+...+q^n=\dfrac{1-q^{n+1}}{1-q}$, avec $q=2$.
Déterminons l'entier $n$ tel que $q^n=262144$, on a $n=18$. Donc $S=\dfrac{1-2^{19}}{1-2}=2^{19}-1=524287$. - $S=3-6+12-24+...+192$ est la somme des premiers termes d'une suite géométrique $(u_n)$ de premier terme $u_0=3$ et de raison $q=-2$, le terme général de $(u_n)$ est $u_n=3\times(-2)^n$.
Recherchons l'indice $n$, on a $3\times(-2)^n=192$ $\Leftrightarrow$ $(-2)^n=64$ $\Leftrightarrow$ $n=6$, car on sait que $(-2)^6=2^6=64$.
Donc en appliquant la formule $S_n=u_0+u_1+...+u_n=u_0\times\dfrac{1-q^{n+1}}{1-q}$, avec $n=6$ et $q=-2$, on obtient:
$S=3\times\dfrac{1-(-2)^7}{(1-(-2))}=3\times\dfrac{(1+128)}{3}=129$. - $S=9+3+1+\dfrac{1}{3}...+\dfrac{1}{729}$ est la somme des premiers termes d'une suite géométrique $(u_n)$ de premier terme $u_0=9$ et de raison $q=\dfrac{1}{3}$, le terme général de $(u_n)$ est $u_n=9\times\bigg(\dfrac{1}{3}\bigg)^n$.
Recherchons l'indice $n$, on a $9\times\bigg(\dfrac{1}{3}\bigg)^n=\dfrac{1}{729}$ $\Leftrightarrow$ $\dfrac{9}{3^n}=\dfrac{1}{729}$ $\Leftrightarrow$ $3^n=6561$, donc $n=8$.
Donc en appliquant la formule $S_n=u_0+u_1+...+u_n=u_0\times\dfrac{1-q^{n+1}}{1-q}$, avec $n=8$, $q=\dfrac{1}{3}$ et $u_0=9$, on obtient:
$S=9\times\dfrac{\bigg(1-(\dfrac{1}{3})^9\bigg)}{\bigg(1-(\dfrac{1}{3})\bigg)}=9\times\dfrac{\dfrac{19682}{19683}}{\dfrac{2}{3}}$ $=9\times\dfrac{19682}{19683}\times\dfrac{3}{2}$ $=9\times\dfrac{9841}{19683}\times 3=\dfrac{265707}{19683}=\dfrac{9841}{729}$.
Définition.
Une suite réelle $(u_n)$ est une liste infinie de nombres réels :$u_0,u_1,u_2,.....,u_n,....$.
$u_n$ est le terme général de la suite.
Remarque.
Il y a deux maniéres possibles pour générer des suites de nombres.
Exemples de suites définies par recurrence.
Représentation graphique de $(u_n)$.
Une suite peut être représentée soit:
$u_0=8$, $u_1=7,5$, $u_2=7$, $u_3=6,5$, etc....
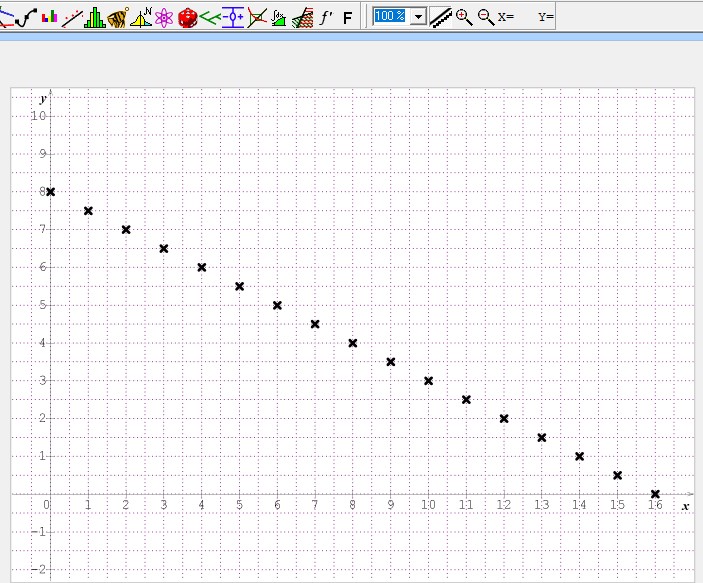
Utilisation d'un tableur.
A l'aide d'une feuille dynamique Géogebra on peut obtenir la valeurs d'un grand nombres de premiers termes d'une suite numérique.
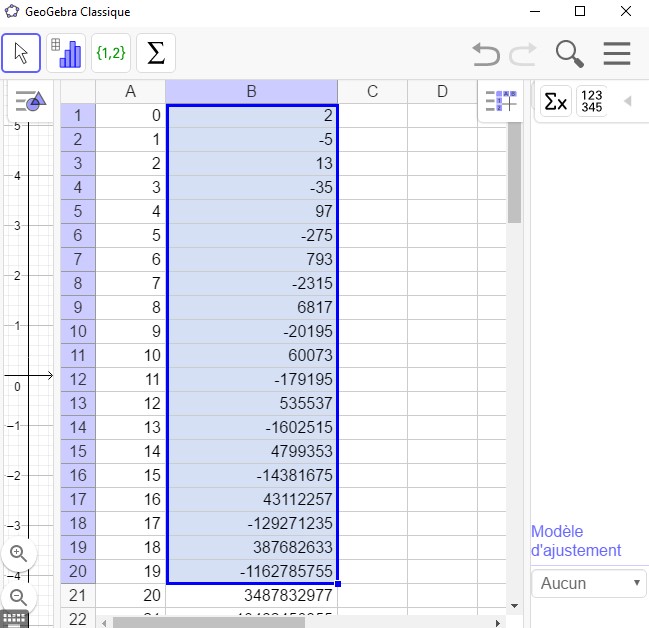
Considérons la suite définie par récurrence $(u_n)$ suivante: $u_0=2$ et $u_{n+1}=(-2)^n-3u_n$.
On a $u_1=(-2)^0-3u_0=1-3\times 2=-5$, $u_2=(-2)^1-3\times u_1=-2-3(-5)=13$, $u_3=(-2)^2-3\times 13=4-39=-35$, etc....Définition et propriétés.
Exercice.
Somme des premiers termes.
On pose $S_n=u_0+u_1+...+u_n$. $S_n$ est la somme des $n+1$ premiers termes de la suite $(u_n)$.
Exercice.
Calculer les sommes suivantes:
Définition et propriétés.
Exercice.
Somme des premiers termes.
On pose $S_n=u_0+u_1+...+u_n$. $S_n$ est la somme des $n+1$ premiers termes de la suite $(u_n)$.
Exercice.
Calculer les sommes suivantes:
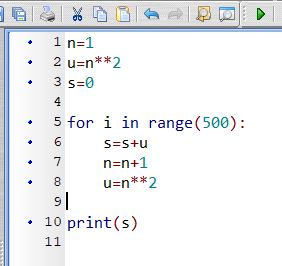
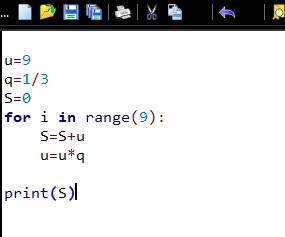
Calcul de $S$, avec un algorithme python.
Prenons deux variables $S$ et $u$. la variable $S$ désigne la somme des premiers termes et $u$ le terme de la suite $(u_n)$ qui est rajouté à chaque fois.
Nous avons le tableau suivant:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 |
| u | 9 | 3 | 1 | $\dfrac{1}{3}\approx0,33$ | $\dfrac{1}{9}\approx 0,11$ | $\dfrac{1}{27}$ | ... | ... | $\dfrac{1}{729}$ |
| S | 0+9=9 | 9+3=12 | 12+1=13 | 13+0,33=13,33 | 13,33+0,11=13,44 | ... | ... | ... | $\approx 13,4993$ |
Exercices classiques sur les suites.
Exercice 1.
Un enfant possède une tirelire avec 700 euros à l'intérieur, chaque année les grand-parents lui donnent entre les fêtes et son anniversaire 350 euros.
On note $u_n$ la somme dans la tirelire après $n$ années d'économie.
- Calculer $u_1$, $u_2$.
- Pour tout $n\in\mathbb{N}$, exprimer $u_{n+1}$ en fonction de $u_n$. en déduire la nature de la suite $(u_n)$.
- Exprimer $T_n$ en fonction de $n$.
Exercice 2.
Pour stoker desphotos numériques, on utilise un algorithme de compression. On estime qu'à chaque niveau de compression, la taille diminue de $21,4\%$.
La taille initiale de la photo est de 4Mo. On pose $T_0=4$ et pour tout $n\in\mathbb{N}$, on désigne par $T_n$ la taille de la photo après $n$ compression.
- Calculer $T_1$, $T_2$.
- Pour tout $n\in\mathbb{N}$, exprimer $T_{n+1}$ en fonction de $T_n$. en déduire la nature de la suite $(T_n)$.
- Exprimer $T_n$ en fonction de $n$.
- Peut-on stocker 20 000 photos sur une clé USB d'une capacité de 32Go? Avec quelle compression?
- $T_1=T_0\times\bigg(1-\dfrac{21,4}{100}\bigg)=T_0\times 0,786$ $=4\times 0,786=3.144$.
$T_2=T_1\times\bigg(1-\dfrac{21,4}{100}\bigg)=T_1\times 0,786$ $\approx 2,471$. - Pour tout $n\in\mathbb{N}$, on a $T_{n+1}=T_n\times\bigg(1-\dfrac{21,4}{100}\bigg)=T_n\times 0,786$. La suite $(T_n)$ est géométrique de raison $q=0,786$.
- Pour tout $n\in\mathbb{N}$, $T_n=T_0\times q^n=4\times (0,786)^n$.
- 32Go=32000Mo, donc chaque photo doit prendre 32000/2000 Mo, donc 1,6mo.
Recherchons le plus petit entier tel que $u_n\leq 1,6$. Avec la calculatrice on trouve $n=4$.
Il faut donc réaliser quatre niveaux de compression, pour que les 20000 photos contiennent dans la clé USB.
- $u_1=u_0+r=700+350=1050$ .
$u_2=u_1+r=1050+350=1400$. - Pour tout $n\in\mathbb{N}$, on a $u_{n+1}=u_n+350$. La suite $(u_n)$ est géométrique de raison $r=350$.
- Pour tout $n\in\mathbb{N}$, $u_n=u_0+nr=700+350n$.
Utilisation d'un algorithme pour calculer la somme des premiers termes d'une suite.
Exemple.
On désire calculer la somme $S=1+4+9+16+...+i^2+...+250000$.
Cette somme peut-être vue comme la somme des premier terme de la suite $(u_n)$ de terme général $u_n=n^2$. Le premier terme sera $u_1=1^2=1$.
On remarque que $250000=(500)^2$, donc $250000=u_{500}$.
Conclusion: $S=u_1+u_2+...+u_{500}$