Comparaison des fonctions usuelles.
Comparaison de fonctions.
- Factoriser l'expression algébrique $f(x)-g(x)$.
- Etudier le signe de $f(x)-g(x)$ en fonction de $x$, en utilisant un tableau de signes.
- Conclure quant à la position relative des deux courbes en regardant le signe de la différence $f(x)-g(x)$.
- Montrer que pour tout $x\in\mathbb{R}$ on a, $f(x)=(x+1)(x-5)$ et $g(x)=(x+1)(-5x+7)$.
- Factoriser $h(x)=f(x)-g(x)=(x+1)(x-5)-(x+1)(-5x+7)$
- A l'aide d'un tableau de signes étudier le signe de $h(x)=f(x)-g(x)$ et en déduire la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$.
- Représenter les deux courbes dans un même repère orthonormée.
- $(x+1)(x-5)=x^2-5x+x-5=x^2-4x-5=f(x)$.
$(x+1)(-5x+7)=-5x^2+7x-5x+7=-5x^2+2x+7=g(x)$ - $h(x)=f(x)-g(x)=(x+1)(x-5)-(x+1)(-5x+7)=(x+1)[(x-5)-(-5x+7)]=(x+1)(6x-12)$.
Etudions le signe de $h(x)=(x+1)(6x-12)$.$x+1=0$ $\Leftrightarrow$ $x=-1$.
$6x-12=0$ $\Leftrightarrow$ $x=2$.Nous en déduisons du tableau de signe ci-contre, la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$.


Courbes représentatives des fonctions $f$ et $g$.

Comparaison de la fonction $x\mapsto x$ et $x\mapsto x^2$.
- Pour tout $x\in[0;1]$ on a $x^2\leq x$.
- Si $0\leq x\leq 1$, alors $\mathcal{C}_g$ est en dessous de $\mathcal{C}_f$ .
- Pour tout $x\in[1;+\infty[$ on a $x^2\geq x$.
- Si $x\in[1;+\infty[$, alors $\mathcal{C}_g$ est au dessus de $\mathcal{C}_f$.
- Factorisons $h(x)=x^2-x$. Nous avons donc $h(x)=x^2-x=x(x-1)$
Etudions le signe de $h(x)=x^2-x$.(A l'aide d'un tableau de signes.)
Nous en déduisons du tableau de signes ci-contre, la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$.


Comparaison de la fonction $x\mapsto x$ et $x\mapsto\sqrt{x}$.
- Pour tout $x\in[0;1]$ on a $x\leq\sqrt{x}$.
- Si $0\leq x\leq 1$, alors $\mathcal{C}_f$ est en dessous de $\mathcal{C}_g$ .
- Pour tout $x\in[1;+\infty[$ on a $x\geq\sqrt{x}$.
- Si $x\in[1;+\infty[$, alors $\mathcal{C}_f$ qui est au dessus de $\mathcal{C}_g$.
- Factorisons $x-\sqrt{x}$. Nous avons la factorisation suivante pour tout $x\geq 0$, $x-\sqrt{x}=\sqrt{x}(\sqrt{x}-1)$.
Etudions le signe de $x-\sqrt{x}=\sqrt{x}(\sqrt{x}-1)$.(A l'aide d'un tableau de signes.)
Nous savons que pour tout $x\geq 0$ , $\sqrt{x}\geq 0$.
Et nous avons les équivalences suivantes: $\sqrt{x}-1>0$ $\Leftrightarrow$ $\sqrt{x}>1$ $\Leftrightarrow$ $x>1$.Nous en déduisons du tableau de signe ci-contre, la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$.

Récapitulatif: Position relative des courbes de $x\to x$, $x\to x^2$ et $x\to\sqrt{x}$.
- Pour tout $x\in[0;1]$ on a $x^2\leq x\leq\sqrt{x}$.
- Si $0\leq x\leq 1$, alors $\mathcal{C}_g$ est en dessous de $\mathcal{C}_f$ qui est en dessous de $\mathcal{C}_h$.
- Pour tout $x\in[1;+\infty[$ on a $\sqrt{x}\leq x\leq x^2$.
- Si $0\leq x\leq 1$, alors $\mathcal{C}_h$ est en dessous de $\mathcal{C}_f$ qui est en dessous de $\mathcal{C}_g$.
Remarque.
Comparer deux fonctions $f$ et $g$, correspond au questionnement suivant: Pour quels $x$ dans $\mathbb{R}$ la courbe de $f$ est-elle en dessous de celle de $g$ et pour quels $x$ dans $\mathbb{R}$ la courbe de $f$ est-elle au dessus de celle de $g$. Pour répondre à cette question, invariablement nous utilisons la méthode suivante:
Méthode.
Exemple.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^2-4x-5$ et soit $g$ la fonction définie sur $\mathbb{R}$ par $g(x)=-5x^2+2x+7$.
Notons $\mathcal{C}_f$ et $\mathcal{C}_g$ les courbes représentatives respectives de $f$ et $g$.
Propriétés.
Soit $f$ et $g$ les fonctions définies sur $[0;+\infty[$ par $f(x)=x$, $g(x)=x^2$.
On note $\mathcal{C}_f$ et $\mathcal{C}_g$ leur courbe représentative respective dans un repère $(O;\vec{i};\vec{j})$.
Nous avons les propriétés suivantes:
Interprétation graphique:

Propriétés.
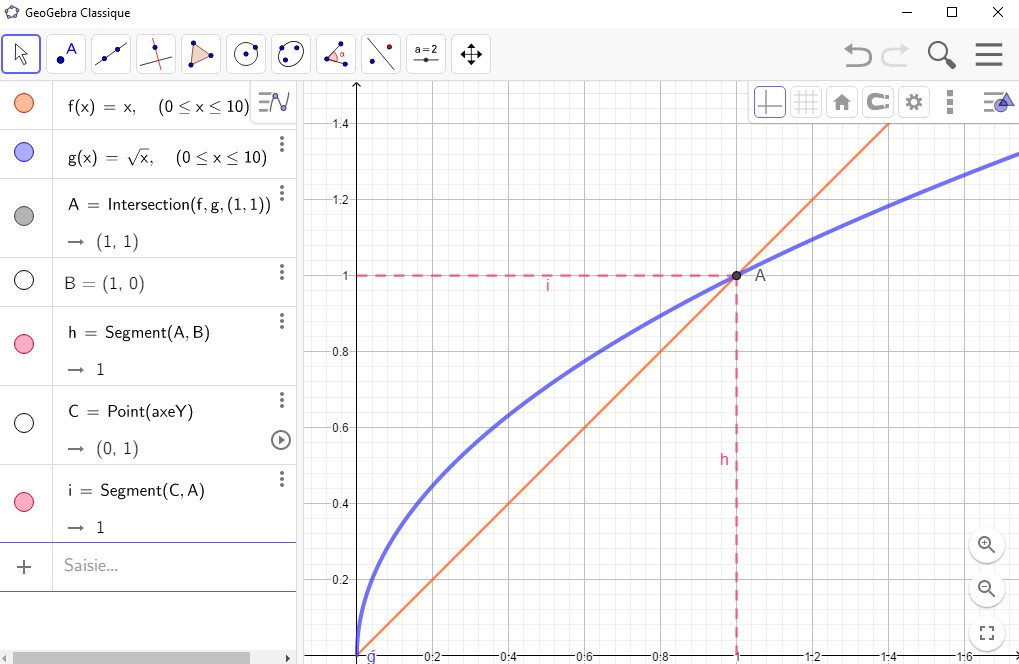
Soit $f$ et $g$ les fonctions définies sur $[0;+\infty[$ par $f(x)=x$, $g(x)=\sqrt{x}$.
On note $\mathcal{C}_f$ et $\mathcal{C}_g$ leur courbe représentative respective dans un repère $(O;\vec{i};\vec{j})$.
Nous avons les propriétés suivantes:
Interprétation graphique:

Propriétés.
Soit $f$, $g$, $h$ les fonctions définies sur $[0;+\infty[$ par $f(x)=x$, $g(x)=x^2$ et $h(x)=\sqrt{x}$.\newline On note $\mathcal{C}_f$, $\mathcal{C}_g$ et $\mathcal{C}_h$ leur courbe représentative respective dans un repère $(O;\vec{i};\vec{j})$. Nous avons les propriétés suivantes:
Interprétation graphique:
