Coordonnées dans le plan.
Repère orthonormé du plan.
Coordonnées du milieu d'un segment.
Propriété.
Dans le repère $(O;I;J)$, on considère les points $A(x_A;y_A)$, et $B(x_B;y_B)$.
- Les coordonnées du milieu $I$ du segment $[AB]$ sont $\bigg(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\bigg)$.
- On note cela par $I\bigg(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\bigg)$ ou bien $I\begin{pmatrix}\dfrac{x_A+x_B}{2}\\ \dfrac{y_A+y_B}{2}\\ \end{pmatrix}$.
Exemple.
Soit $A(-3-2)$ et $B(6;4)$, le milieu $I$ du segment $[AB]$ a pour coordonnées:
$I\begin{pmatrix}\dfrac{x_A+x_B}{2}\\ \dfrac{y_A+y_B}{2}\\ \end{pmatrix}\begin{pmatrix}\dfrac{-3+6}{2}\\ \dfrac{-2+4}{2}\\ \end{pmatrix}$ $\begin{pmatrix}\dfrac{3}{2}\\ 1\\ \end{pmatrix}$.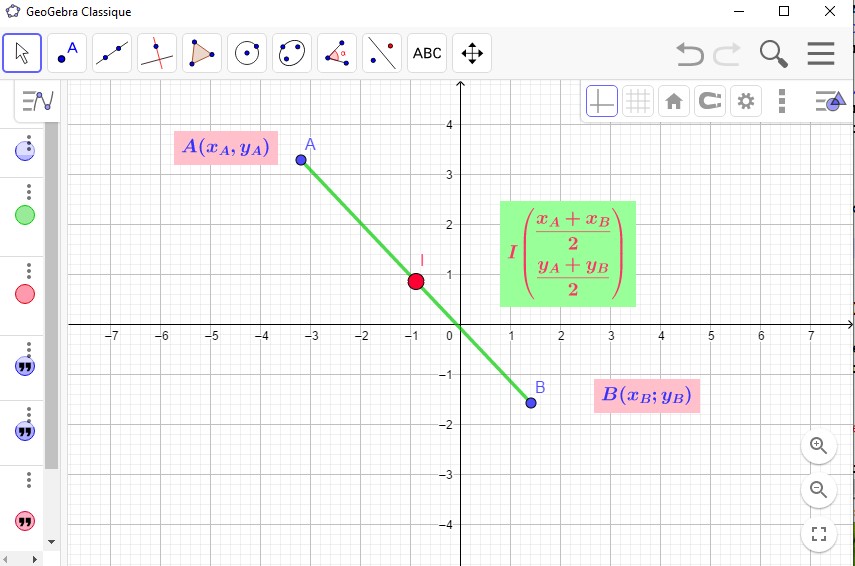
Soit $I$ le milieu du segment $[AB]$, donc nous avons l'égalité vectorielle $\overrightarrow{AI}=\overrightarrow{IB}$. La démonstration a utilisé l'outil vectoriel pour rappel voir:
$\overrightarrow{AI}\begin{pmatrix} x_I-x_A\\y_I-y_A\\ \end{pmatrix}$ et $\overrightarrow{IB}\begin{pmatrix} x_B-x_I\\y_B-y_I\\ \end{pmatrix}$.
Donc $\overrightarrow{AI}=\overrightarrow{IB}$ $\Leftrightarrow$ $\begin{pmatrix} x_I-x_A\\y_I-y_A\\ \end{pmatrix}=\begin{pmatrix} x_B-x_I\\y_B-y_I\\ \end{pmatrix}$.
Remarque:
Ici les nombres connus sont les nombres $x_A$; $y_A$; $x_B$ et $y_B$ et les nombres inconnus sont $x_I$ et $y_I$.
Nous avons donc deux équations distinctes à résoudre, chacune ayant pour inconnus $x_I$ ou $y_I$.- $x_I-x_A=x_B-x_I$ $\Leftrightarrow$ $2x_I=x_A+x_B$ $\Leftrightarrow$ $x_I=\dfrac{x_A+x_B}{2}$
- $y_I-y_A=y_B-y_I$ $\Leftrightarrow$ $2y_I=y_A+y_B$ $\Leftrightarrow$ $y_I=\dfrac{y_A+y_B}{2}$
Généralités sur les vecteurs. Vecteurs dans un repère. Distance entre deux points dans un repère orthonormé.
- On remarque que le segment $[AH]$ est parralèle à l'axe des abscisses, on a: $AH^2=(x_B-x_A)^2$.
- On remarque que le segment $[BH]$ est parralèle à l'axe des ordonnées, on a: $BH^2=(y_B-y_A)^2$
Utilisation des formules.
- Montrons de deux façons différentes que le quadrilatère $ABCD$ est un parallélogramme
-
- $\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\y_B-y_A\\ \end{pmatrix}\begin{pmatrix} 1+3\\-1+2\\ \end{pmatrix}\begin{pmatrix} 4\\1\\ \end{pmatrix}$
- $\overrightarrow{DC}\begin{pmatrix} x_C-x_D\\y_C-y_D\\ \end{pmatrix}\begin{pmatrix} 4-0\\4-3\\ \end{pmatrix}\begin{pmatrix} 4\\1\\ \end{pmatrix}$
- $\overrightarrow{AB}=\overrightarrow{DC}$,
- $ABCD$ est donc un parallélogramme.
- $I\begin{pmatrix}\dfrac{x_A+x_C}{2}\\\dfrac{y_A+y_C}{2}\\ \end{pmatrix}\begin{pmatrix}\dfrac{-3+4}{2}\\\dfrac{-2+4}{2}\\ \end{pmatrix}=\begin{pmatrix}\dfrac{1}{2}\\1\\ \end{pmatrix}$
- $J\begin{pmatrix}\dfrac{x_B+x_D}{2}\\\dfrac{y_B+y_D}{2}\\ \end{pmatrix}=\begin{pmatrix}\dfrac{1+0}{2}\\\dfrac{-1+3}{2}\\ \end{pmatrix}=\begin{pmatrix}\dfrac{1}{2}\\1\\ \end{pmatrix}$
- $[AC]$ et $[BD]$ ont le même milieu,
- $ABCD$ est donc un parallélogramme.
Figure.
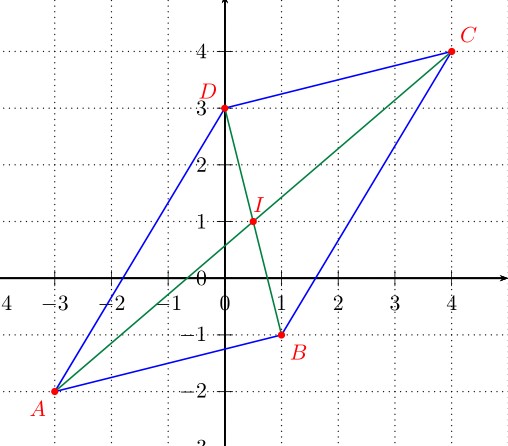
Quelle est la nature du triangle $ABD$ ?
- $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{4^2+1^2}=\sqrt{17}$,
- $AD=\sqrt{(x_D-x_A)^2+(y_D-y_A)^2}=\sqrt{3^2+5^2}=\sqrt{34}$,
- $DB=\sqrt{(x_B-x_D)^2+(y_B-y_D)^2}=\sqrt{1^2+(-4)^2}=\sqrt{17}$,
- $AB=DB$ et $AD^2=AB^2+BD^2$ donc $ABD$ est donc un triangle rectangle isocèle en $B$.
Algorithme et géométrie
Propriété.
Dans le repère $(O;I;J)$ orthonormée, on considère les points $A(x_A;y_A)$, et $B(x_B;y_B)$.
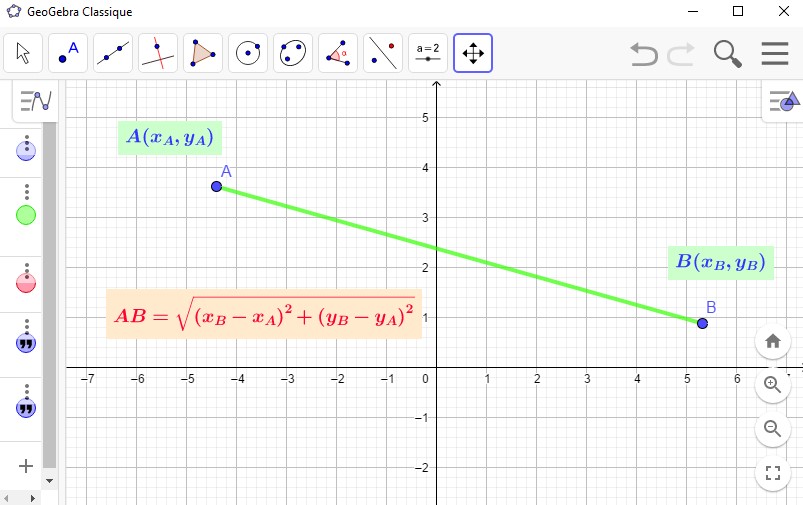
La distance entre les points A et B que l'on note $AB$ ou bien $d(A,B)$ est égale à:
$\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$.
Exemple.
Soit $A(-3-2)$ et $B(6;4)$, calculons la longueur du segment $[AB]$:
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$.
Donc on a $AB=\sqrt{(6-(-3))^2+(4-(-2))^2}=\sqrt{9^2+6^2}$ $=\sqrt{81+36}=\sqrt{117}$.
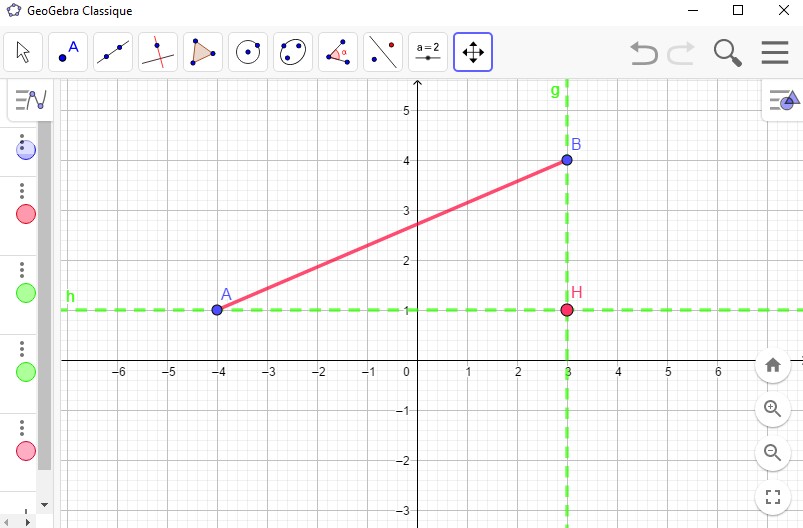
$AB^2=AH^2+BH^2$.
Exemple.
Dans un repère $(O;I;J)$, on considère les points $A(-3;-2)$, $B(1;-1)$, $C(4;4)$ et $D(0;3)$.
Algorithme calculant la distance entre deux points $A$ et $B$.
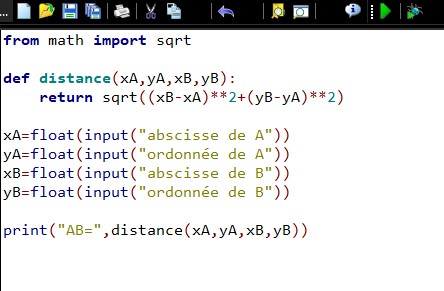
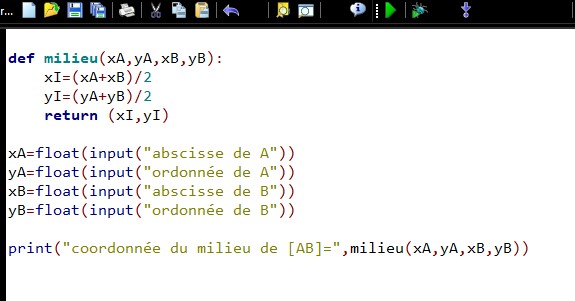
Algorithme calculant les coordonnées du milieu de $[AB]$.