Vecteurs du plan.
Translations et vecteurs.
Définition.
- Un point $C$ est l’image d’un point $D$ par la translation qui transforme $A$ en $B$ lorsque le quadrilatère $ABCD$ est un parallélogramme.
- On dit alors que $C$ est l’image du point $D$ par la translation de vecteur $\overrightarrow{AB}$.
Proposition.
Soit la translation de vecteur $\overrightarrow{AB}$ transformant $D$ en $C$. Nous avons les propriétés suivantes:
- $(AB)$ et $(DC)$ sont parallèles (même direction),
- $AB$ et $DC$ sont de même longueur,
- $\overrightarrow{AB}$ et $\overrightarrow{DC}$ vont dans le même sens.
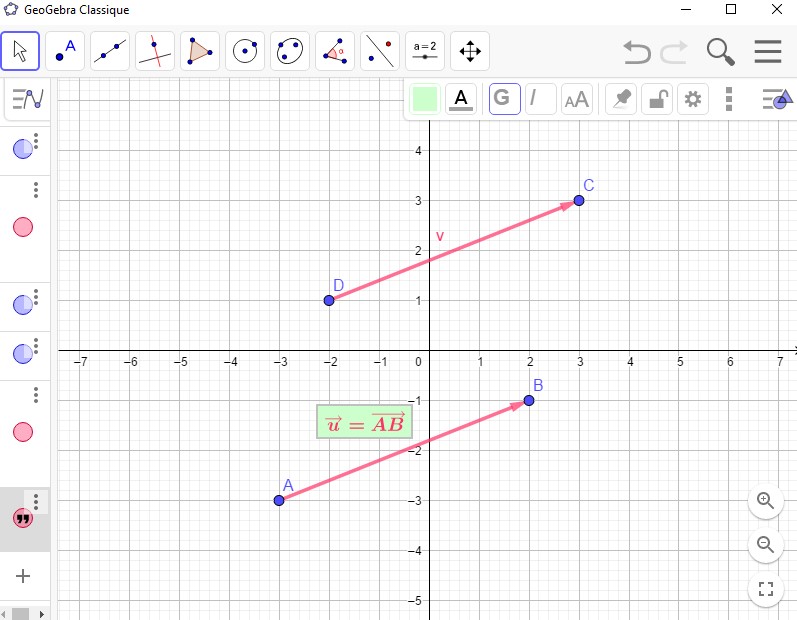
Égalité de deux vecteurs.
Soit quatre points A, B, C et D du plan. les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont égaux signifie que $D$ est l'image de $C$ par la translation de vecteur $\overrightarrow{AB}$. On note $\overrightarrow{AB}=\overrightarrow{CD}$.
Propriétés.
- les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ sont égaux si et seulement si le quadrilatère $ABCD$ est un parallélogramme (éventuellement aplati).
- les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ sont égaux si et seulement si les segments $[AC]$ et $[BD]$ ont même milieu.
Exemples:
Nous avons les égalités suivantes:- $\overrightarrow{AB}=\overrightarrow{CD}$ $=\overrightarrow{EF}$.
$\overrightarrow{GH}=\overrightarrow{IJ}$ - Mais aussi nous avons par exemple:
$\overrightarrow{AE}=\overrightarrow{BF}$
et $\overrightarrow{GI}=\overrightarrow{HJ}$


Opposé d'un vecteur
Somme de deux vecteurs.
- $\overrightarrow{AB} = \overrightarrow{0}$ si et seulement si $A=B$,
- Si on fixe un point $O$, alors pour tout vecteur $\overrightarrow{u}$, il existe un unique point $M$ vérifiant $\overrightarrow{u} = \overrightarrow{OM}$.
Savoir tracer la somme de deux vecteurs.
La relation de Chasles.
- Relation de Chasles : Pour tous points $A$, $B$ et $C$ du plan, on a $\overrightarrow{AB}+\overrightarrow{BC}= \overrightarrow{AC}$.
- Nous avons la relation $\overrightarrow{AB}+\overrightarrow{AC}= \overrightarrow{AD}$ si et seulement si $ABCD$ est un parallélogramme.
- $\overrightarrow{u}+\overrightarrow{v} =\overrightarrow{v}+\overrightarrow{u}$,
- $(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w} =\overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})$,
- $\overrightarrow{u}+\overrightarrow{0} =\overrightarrow{u}$.
Différence de deux vecteurs.
Définition.
Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs.
La différence des vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, notée $\overrightarrow{u}-\overrightarrow{v}$, est le vecteur égal à la somme $\overrightarrow{u}+(-\overrightarrow{v})$.Méthode pour tracer la somme de deux vecteurs
Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs, on construit le vecteur $\overrightarrow{w} =\overrightarrow{u}-\overrightarrow{v}$ de la façon suivante : Soit $A$ un point du plan, on trace le représentant de $\overrightarrow{u}$ d'origine $A$ : il a pour extrémité $B$, puis on trace le représentant de $-\overrightarrow{v}$ d'origine $B$ : il a pour extrémité $D$. Le vecteur $\overrightarrow{AD}$ est un représentant du vecteur $\overrightarrow{w}$.
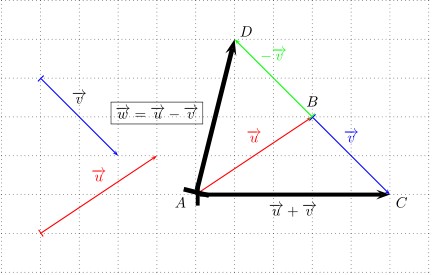
Savoir tracer la différence de deux vecteurs.
Multiplication d'un vecteur par un nombre réel.
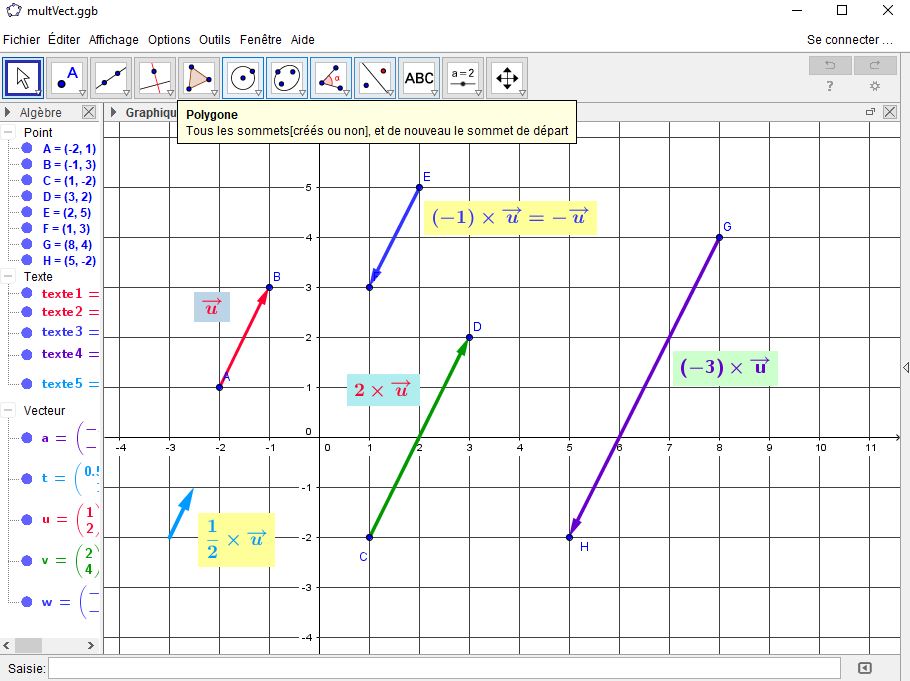
- $A$, $B$ et $C$ sont alignés,
- si $k>0$, $AC =kAB$ et $B$ et $C$ sont du même côté par rapport à $A$,
- Si $k < 0$, $AC =-kAB$ et $B$ et $C$ sont de part et d'autre de $A$.
- Si $\overrightarrow{u} = 0$ ou $k=0$ alors $\overrightarrow{v} = \overrightarrow{0}$.
- $k(\overrightarrow{u} + \overrightarrow{v}) = k\overrightarrow{u} + k\overrightarrow{v}$.
- $(k+l)\overrightarrow{u} = k\overrightarrow{u} +l\overrightarrow{u}$
- $k(\lambda\overrightarrow{u}) = (k\lambda)\overrightarrow{u}$
- $k\overrightarrow{u} = \overrightarrow{0} \Longleftrightarrow k=0$ ou $\overrightarrow{u} =\overrightarrow{0}$
Colinéarité de deux vecteurs.
Définition.
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires s'il existe un réel $k$ non nul tel que $\overrightarrow{v}=k\overrightarrow{u}$.
Propriété.
- Trois points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
- Deux droites $(AB)$ et $(CD)$ sont parallèles si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont colinéaires.
Définition.
Quels que soient les points $A$ et $B$, le vecteur $\overrightarrow{BA}$ est appelé vecteur opposé au vecteur $\overrightarrow{AB}$.
Si $\overrightarrow{u} =\overrightarrow{AB}$, alors $-\overrightarrow{u} =\overrightarrow{BA}$.
Définition.
Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs. La somme des vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, notée $\overrightarrow{u}+\overrightarrow{v}$, est le vecteur associée à la translation résultant de l'enchaînement des translations de vecteur $\overrightarrow{u}$ et de vecteur $\overrightarrow{v}$.
Méthode pour tracer la somme de deux vecteurs
Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs, on construit le vecteur $\overrightarrow{w} =\overrightarrow{u}+\overrightarrow{v}$ de la façon suivante : Soit $A$ un point du plan, on trace le représentant de $\overrightarrow{u}$ d'origine $A$ : il a pour extrémité $B$, puis on trace le représentant de $\overrightarrow{v}$ d'origine $B$ : il a pour extrémité $C$. Le vecteur $\overrightarrow{AC}$ est un représentant du vecteur $\overrightarrow{w}$.

Le vecteur nul $\overrightarrow{0}$.
Place le représentant du vecteur $\overrightarrow{u}+\overrightarrow{v}$ ayant pour origine le point A.
Barême: $2\times1$ pts pour le tracé de $\overrightarrow{u}$ et $\overrightarrow{v}$ et deux points pour le tracé de la somme.| $\overrightarrow{u}$ |
| $\overrightarrow{v}$ |
| A |
note:
Proposition.
Place le représentant du vecteur $\overrightarrow{u}-\overrightarrow{v}$ ayant pour origine le point A.
Barême: $2\times1$ pts pour le tracé de $\overrightarrow{u}$ et $\overrightarrow{v}$ et deux points pour le tracé de la somme.| $\overrightarrow{u}$ |
| $\overrightarrow{v}$ |
| A |
note:
Définition.
Soit $\overrightarrow{u} =\overrightarrow{AB}$ un vecteur non nul et $k$ un réel non nul, on définit le vecteur $\overrightarrow{v} = k\overrightarrow{u} =\overrightarrow{AC}$ par :
Propriétés.
Quels que soient les vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et les réels $k$ et $l$ , on a :