Vecteurs dans un repère.
coordonnées d'un vecteur dans un repère quelconque.
Savoir placer un vecteur dans un repère.
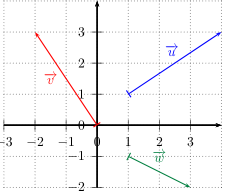
- On peut écrire $\overrightarrow{u}(3;2)$ ou bien $\overrightarrow{u}\begin{pmatrix}3\\2\\ \end{pmatrix}$
- On peut écrire $\overrightarrow{v}(-2;3)$ ou bien $\overrightarrow{v}\begin{pmatrix}-2\\3\\ \end{pmatrix}$
- On peut écrire $\overrightarrow{w}(2;-1)$ ou bien $\overrightarrow{w}\begin{pmatrix}2\\-1\\ \end{pmatrix}$
Coordonnées et calculs sur les vecteurs.
- Egalité de deux vecteurs :
Deux vecteurs sont égaux si et seulement si leurs coordonnées sont égales.
$\overrightarrow{u}=\overrightarrow{v}$ $\Longleftrightarrow$ $\bigg\{ \begin{array}[pos]{c} x=x'\\ y=y'\\ \end{array}$. - Somme de deux vecteurs : Le vecteur $\overrightarrow{w}=\overrightarrow{u}+\overrightarrow{v}$ a pour coordonnées $\overrightarrow{w}\begin{pmatrix}x+x'\\y+y'\\ \end{pmatrix}$. On peut aussi écrire $\overrightarrow{w}(x+x';y+y')$.
- Produit d'un vecteur par un réel : Le vecteur $\overrightarrow{w}=k\overrightarrow{u}$ a pour coordonnées $\overrightarrow{w}\begin{pmatrix}kx\\ky\\ \end{pmatrix}$. On peut aussi écrire $\overrightarrow{w}(kx;ky)$.
- En classe de seconde nous admettrons cette propriété.
- Soient deux vecteurs $\overrightarrow{u}$ $\overrightarrow{v}$ de coordonnées respectives $(x;y)$ et $(x';y')$ dans un repère $(O;\overrightarrow{i};\overrightarrow{j})$.
Par définition nous savons que nous avons:- $\overrightarrow{u}=x\times\overrightarrow{i}+y\times\overrightarrow{j}$.
- $\overrightarrow{v}=x'\times\overrightarrow{i}+y'\times\overrightarrow{j}$.
Regroupons les termes entre eux.
$(x\times\overrightarrow{i}+y\times\overrightarrow{j})+(x'\times\overrightarrow{i}+y'\times\overrightarrow{j})$ $=(x\times\overrightarrow{i}+x'\times\overrightarrow{i})+(y\times\overrightarrow{j}+y'\times\overrightarrow{j})$ $=(x+x')\times\overrightarrow{i}+(y+y')\times\overrightarrow{j}$.
Donc le vecteur $\overrightarrow{w}=\overrightarrow{u}+\overrightarrow{v}$ a pour coordonnées $\begin{pmatrix}x+x'\\y+y'\\ \end{pmatrix}$ - Soit un vecteur $\overrightarrow{u}$ de coordonnées $(x;y)$ dans un repère $(O;\overrightarrow{i};\overrightarrow{j})$.
$k\times\overrightarrow{u}=k\times(x\times\overrightarrow{i}+y\times\overrightarrow{j})$ $=k\times(x\times\overrightarrow{i})+k\times(y\times\overrightarrow{j})$. $=(kx)\times\overrightarrow{i}+(ky)\times\overrightarrow{j}$.
Donc le vecteur $\overrightarrow{w}=k\overrightarrow{u}$ a pour coordonnées $\overrightarrow{w}\begin{pmatrix}kx\\ky\\ \end{pmatrix}$. - $\overrightarrow{v}=\overrightarrow{w}$ $\Longleftrightarrow$ $\bigg\{\begin{array}[pos]{c}5a&=&5\\6b&=&3\\\end{array}$ $\Longleftrightarrow $ $\bigg\{\begin{array}[pos]{c}a&=&1\\b&=&\frac{1}{2}\\ \end{array}$
- $\overrightarrow{u}+\overrightarrow{v}\begin{pmatrix}1+5\\-3+3\\ \end{pmatrix}=\begin{pmatrix}6\\0\\ \end{pmatrix}$
- $-\overrightarrow{u}\begin{pmatrix}-1\\3\\ \end{pmatrix}$
- $5\overrightarrow{v}\begin{pmatrix}5\times 5\\5\times 3\\ \end{pmatrix}=\begin{pmatrix}25\\15\\ \end{pmatrix}$
- $-\overrightarrow{u}+5\overrightarrow{v}\begin{pmatrix}-1+25\\3+15\\ \end{pmatrix}=\begin{pmatrix}24\\18\\ \end{pmatrix}$
- $\overrightarrow{OA}=x_A\times\overrightarrow{i}+y_A\times\overrightarrow{j}$.
- $\overrightarrow{OB}=x_B\times\overrightarrow{i}+y_B\times\overrightarrow{j}$.
- Soit $A(3;2)$ et $B(1;-1)$. On a $\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\y_B-y_A\\ \end{pmatrix}$ $=\begin{pmatrix} 1-3\\-1-2\\ \end{pmatrix}$ $=\begin{pmatrix} -2\\-3\\ \end{pmatrix}$
- Soit $P(13;2)$ et $Q(1;-1)$. On a $\overrightarrow{QP}\begin{pmatrix} x_P-x_Q\\y_P-y_Q\\ \end{pmatrix}$ $=\begin{pmatrix} 13-1\\2-(-1)\\ \end{pmatrix}$ $=\begin{pmatrix} 12\\3\\ \end{pmatrix}$
Colinéarité de deux vecteurs.
- Les vecteurs non nuls $\overrightarrow{u}\begin{pmatrix}x\\y\\ \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix}x'\\y'\\ \end{pmatrix}$ sont colinéaires si et seulement si $\overrightarrow{v} =k\overrightarrow{u}$ c'est à dire les coordonnées de $\overrightarrow{u}$ et $\overrightarrow{v}$ sont proportionnelles.
- Dans un repère quelconque, deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ sont colinéaire si et seulement si on a: $x\times y'-x'\times y=0.$
- Les vecteurs $\overrightarrow{u}\begin{pmatrix}2\\4\\ \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix}1\\2\\ \end{pmatrix}$ sont colinéaires car $\overrightarrow{u}=2\overrightarrow{v}$. On considère les trois vecteurs du plan suivants : $\overrightarrow{u}\begin{pmatrix}2\\-3\\ \end{pmatrix}$, $\overrightarrow{v}\begin{pmatrix}-6\\9\\ \end{pmatrix}$ et $\overrightarrow{w}\begin{pmatrix}5\\-7\\ \end{pmatrix}$.
- Les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires car $2\times9-(-3)\times(-6)=18-18=0$,
- Les vecteurs $\overrightarrow{u}$ et $\overrightarrow{w}$ ne sont pas colinéaires car $2\times(-7)-(-3)\times5=-14+15=1\neq0$.
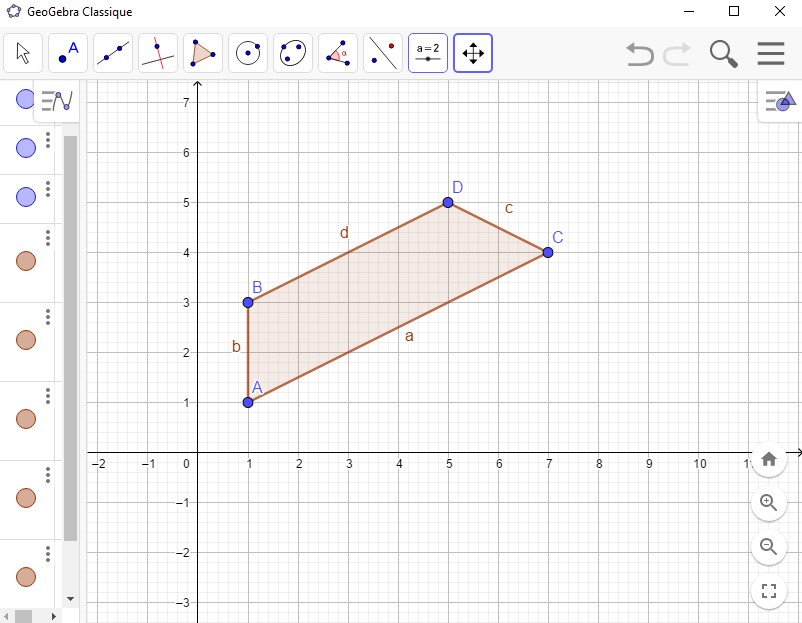
- $\overrightarrow{AC}\begin{pmatrix}7-1\\4-1\\ \end{pmatrix}=\begin{pmatrix}6\\3\\ \end{pmatrix}$,
- $\overrightarrow{BD}\begin{pmatrix}5-1\\5-3\\ \end{pmatrix}=\begin{pmatrix}4\\2\\ \end{pmatrix}$,
- $XY'-YX'= 6\times 2-3\times 4=0$.
Les vecteurs $\overrightarrow{AC}$ et $\overrightarrow{BD}$ sont colinéaires, donc les droites $(AC)$ et $(BD)$ sont donc parallèles.
Le quadrilatère $ABCD$ est un trapèze.
Théorème.
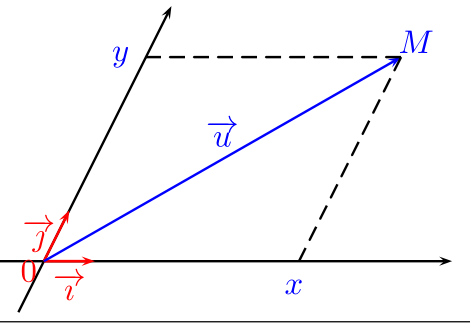
Dans le repère $(O;\overrightarrow{i};\overrightarrow{j})$, les coordonnées d'un vecteur $\overrightarrow{u}$ sont les coordonnées de l'unique point $M$ tel que $\overrightarrow{u} =\overrightarrow{OM}$. On note cela par $\overrightarrow{u}(x;y)$ ou bien $\overrightarrow{u}\begin{pmatrix}x\\y\\ \end{pmatrix}$.
Remarque.
Bien souvent,le repère $(O;\overrightarrow{i};\overrightarrow{j})$ peut ne pas être orthonormé, mais quelconque comme dans l'illustration ci-contre.
On a l'égalité vectorielle:$\overrightarrow{OM}=x\times\overrightarrow{i}+y\times\overrightarrow{j}$.
Exemples de vecteurs.
Place dans le quadrillage ci-dessous les vecteurs de coordonnées suivantes
Il faudra cliquer sur le quadrillage pour placer les points qui constituent le vecteur!| $\overrightarrow{u}$ |
| $\overrightarrow{v}$ |
| $\overrightarrow{w}$ |
| $\overrightarrow{t}$ |
note:
Propositions.
-
Soient deux vecteurs $\overrightarrow{u}$ $\overrightarrow{v}$ de coordonnées respectives $(x;y)$ et $(x';y')$.
Exemples.
Soient les vecteurs $\overrightarrow{u}\begin{pmatrix}1\\-3\\ \end{pmatrix}$, $\overrightarrow{v}\begin{pmatrix}5\\3\\ \end{pmatrix}$ et $\overrightarrow{w}\begin{pmatrix}5a\\6b\\ \end{pmatrix}$ alors:Théorème.
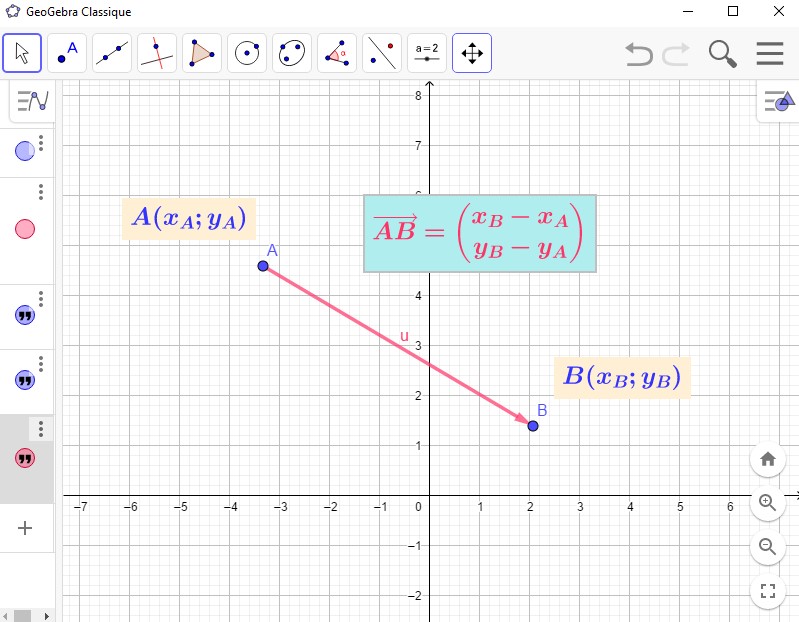
Dans le repère $(O;\overrightarrow{i};\overrightarrow{j})$, on considère les points $A(x_A;y_A)$, et $B(x_B;y_B)$.
Les Coordonnées du vecteur $\overrightarrow{AB}$ sont égales à $\begin{pmatrix} x_B-x_A\\y_B-y_A\\ \end{pmatrix}$. On peut aussi écrire $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$
Dans le repère $(O;\overrightarrow{i};\overrightarrow{j})$, on considère les points $A(x_A;y_A)$, et $B(x_B;y_B)$.
Donc on a $\overrightarrow{AB}=(x_B\times\overrightarrow{i}+y_B\times\overrightarrow{j})-(x_A\times\overrightarrow{i}+y_A\times\overrightarrow{j})$.
Donc $\overrightarrow{AB}=(x_B\times\overrightarrow{i}-x_A\times\overrightarrow{i})+(y_B\times\overrightarrow{j}-y_A\times\overrightarrow{j})$ $=(x_B-x_A)\times\overrightarrow{i}+(y_B-y_A)\times\overrightarrow{j}$.
Donc les Coordonnées du vecteur $\overrightarrow{AB}$ sont égales à $\begin{pmatrix} x_B-x_A\\y_B-y_A\\ \end{pmatrix}$.
Donc on a $\overrightarrow{AB}=(x_B\times\overrightarrow{i}+y_B\times\overrightarrow{j})-(x_A\times\overrightarrow{i}+y_A\times\overrightarrow{j})$.
Donc $\overrightarrow{AB}=(x_B\times\overrightarrow{i}-x_A\times\overrightarrow{i})+(y_B\times\overrightarrow{j}-y_A\times\overrightarrow{j})$ $=(x_B-x_A)\times\overrightarrow{i}+(y_B-y_A)\times\overrightarrow{j}$.
Donc les Coordonnées du vecteur $\overrightarrow{AB}$ sont égales à $\begin{pmatrix} x_B-x_A\\y_B-y_A\\ \end{pmatrix}$.
Exemples.
Théorème.
Place dans le repère ci-contre quatres vecteurs colinéaires au vecteur donné ci-contre.
Il faudra cliquer sur le quadrillage pour placer les points qui constituent le vecteur!$\overrightarrow{u}$
note:
Exemples.
Exercice.
Soient quatre points $A(1;1)$, $B(1;3)$, $C(7;4)$ et $D(5;5)$ du plan.
Quelle est la nature du quadrilatère $ABDC$ ?
correction.
