Loi uniforme, loi exponentielle .
Lois à densités sur un intervalle $I$(borné).
- Si $I=[a;b]$, $P(\mathcal{X}\in I)=\int_a^bf(x)dx$.
- $P(\mathcal{X}=a)=\displaystyle\int_a^af(x)dx=0$.
- $P(\mathcal{X}\leq a)=P(\mathcal{X} < a)$.
- $P(\mathcal{X}\in\mathbb{R})=1=\displaystyle\lim_{A\to+\infty}\displaystyle\int_{-A}^Af(x)dx$.
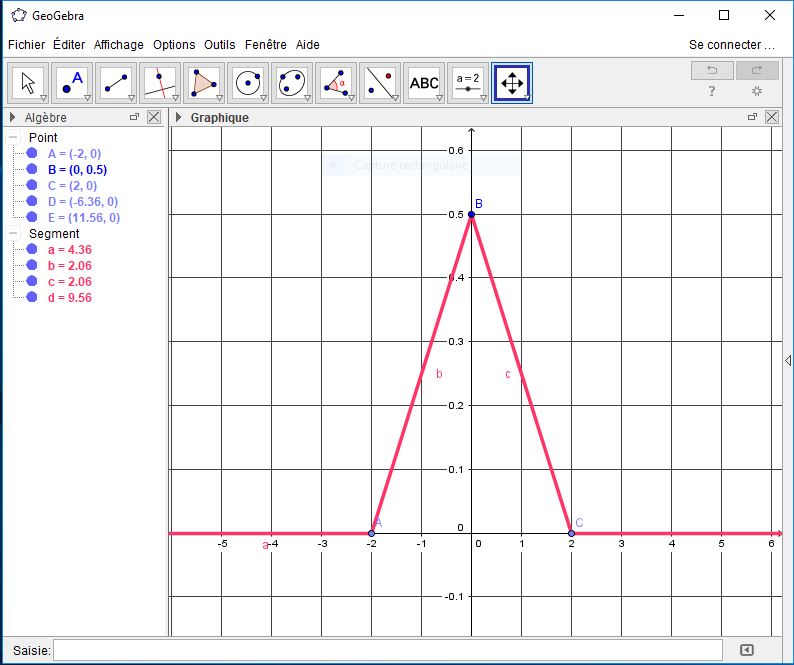
- On remarque que $f(x)=0$ pour tout $x\in]-\infty;-2]\cup [2;+\infty[$. la fonction $f$ est ce que l'on appelle une fonction
affine par morceaux.
Pour tout $x\in[0;2]$, $f(x)=\dfrac{1}{2}-\dfrac{1}{4}x$. Pour tout $x\in[-2;0]$, nous avons $f(x)=\dfrac{1}{2}+\dfrac{1}{4}x$.
Nous avons donc: $f(x)=\Bigg\{ \begin{array}[pos]{c} \dfrac{1}{2}-\dfrac{1}{4}x~~~~si~~~~x\in[0;2]\\ \dfrac{1}{2}+\dfrac{1}{4}x~~~~si~~~~x\in[-2;0]\\ 0~~~~si~~~~x\in]-\infty;-2]\cup [2;+\infty[\\ \end{array} $. - Montrons que $f$ est une fonction de densité.
- Nous remarquons que pour tout $x\in\mathbb{R}$, $f(x)\geq 0$.
- Puisque $f(x)=0$ pour tout $x\in]-\infty;-2]\cup [2;+\infty[$, calculons $\displaystyle\int_{-2}^2f(x)dx$.
$\displaystyle\int_{-2}^2f(x)dx$ $=\displaystyle\int_{-2}^0f(x)dx+\displaystyle\int_{0}^2f(x)dx$ $=\displaystyle\int_{-2}^0\dfrac{1}{2}+\dfrac{1}{4}xdx+\displaystyle\int_{0}^2\dfrac{1}{2}-\dfrac{1}{4}xdx$
$\displaystyle\int_{-2}^2f(x)dx$ $=\bigg[\dfrac{x}{2}+\dfrac{x^2}{8}\bigg]_{-2}^0+\bigg[\dfrac{x}{2}-\dfrac{x^2}{8}\bigg]_{0}^2$ $=[0-(-1+\dfrac{1}{2})]+[(1-\dfrac{1}{2})-0]$ $=1-\dfrac{1}{2}+1-\dfrac{1}{2}=2-1=1$.
Donc $\displaystyle\lim_{A\to+\infty}\displaystyle\int_{-A}^Af(x)dx$ $=\displaystyle\int_{-2}^2f(x)dx=1$. La fonction $f$ peut donc être utilisée comme fonction de densité de probabilité.
- Soit $\mathcal{X}$ la variable aléatoire de fonction de densité $f$.
- $P(\mathcal{X}\leq 1)$ $=\displaystyle\int_{-2}^1f(x)dx$ $=\displaystyle\int_{-2}^0f(x)dx+\displaystyle\int_{0}^1f(x)dx$
$=\dfrac{1}{2}+\bigg[\dfrac{x}{2}-\dfrac{x^2}{8}\bigg]_{0}^1$ $=\dfrac{1}{2}+[(\dfrac{1}{2}-\dfrac{1}{8})-0]$ $=1-\dfrac{1}{8}=\dfrac{7}{8}$.
$P(\mathcal{X} < 1)$ $=P(\mathcal{X}\leq 1)=\dfrac{7}{8}$. - $P(\mathcal{X}\geq 1)$ $=1-P(\mathcal{X} < 1)$ $1-\dfrac{7}{8}=\dfrac{1}{8}$.
Remarque:
Pour calculer $P(\mathcal{X}\geq 1)$ on aurait pu aussi calculer l'intégrale $\displaystyle\int_{1}^2f(x)dx$.
$P(-1 < \mathcal{X}\leq 1.5)$ $=\displaystyle\int_{-1}^{1.5}f(x)dx$ $=\displaystyle\int_{-1}^0\dfrac{1}{2}+\dfrac{1}{4}xdx+\displaystyle\int_{0}^{1.5}\dfrac{1}{2}-\dfrac{1}{4}xdx$ $=\bigg[\dfrac{x}{2}+\dfrac{x^2}{8}\bigg]_{-1}^0+\bigg[\dfrac{x}{2}-\dfrac{x^2}{8}\bigg]_{0}^{1.5}$ $=[0-(-\dfrac{1}{2}+\dfrac{1}{8})]+[(\dfrac{1.5}{2}-\dfrac{1.5^2}{8})-0]$ $=\dfrac{1}{2}-\dfrac{1}{8}+\dfrac{3}{4}-\dfrac{9}{32}$ - Donner l'expression de la fonction $f$ dont la courbe représentative est ci-contre.
- Montrer que $f$ peut être utilisée comme fonction de densité.
- Soit $\mathcal{X}$ la variable aléatoire de fonction de densité $f$.
- Calculer $P(\mathcal{X}\leq 1)$, $P(\mathcal{X} < 1)$.
- Calculer $P(\mathcal{X}\geq 1)$, $P(-1 < \mathcal{X}\leq 1.5)$.
Espérance mathématique d'une variable aléatoire continue.
Définition.
Soit $X$ une variable aléatoire définie sur un univers $\Omega$, de densité la fonction continue $f$ et supposons de plus que l'image de $X$ soit un intervalle $I$, c'est à dire $I=X(\Omega)=[a,b]$.
L'espérance de $X$ est le nombre $E(X)=\displaystyle\int_a^bxf(x)dx$.Exemple.
Reprenons l'exemple de l'exercice précédent avec $f(x)=\Bigg\{ \begin{array}[pos]{c} \dfrac{1}{2}-\dfrac{1}{4}x~~~~si~~~~x\in[0;2]\\ \dfrac{1}{2}+\dfrac{1}{4}x~~~~si~~~~x\in[-2;0]\\ 0~~~~si~~~~x\in]-\infty;-2]\cup [2;+\infty[\\ \end{array} $.
Soit $\mathcal{X}$ la variable aléatoire de densité $f$.
Nous avons $E(\mathcal{X})=\displaystyle\int_{-2}^2xf(x)dx$ $=\displaystyle\int_{-2}^0x(\dfrac{1}{2}+\dfrac{1}{4}x)dx+\displaystyle\int_{0}^2x(\dfrac{1}{2}-\dfrac{1}{4}x)dx$ $=\displaystyle\int_{-2}^0(\dfrac{x}{2}+\dfrac{x^2}{4})dx+\displaystyle\int_{0}^2(\dfrac{x}{2}-\dfrac{x^2}{4})dx$ $=\bigg[\dfrac{x^2}{4}+\dfrac{x^3}{12}\bigg]_{-2}^0+\bigg[\dfrac{x^2}{4}-\dfrac{x^3}{12}\bigg]_{0}^2$ $=$Loi uniforme.
Définition.
Une variable aléatoire $\mathcal{X}$ suit la loi uniforme sur $[a;b]$ lorsque sa densité $f$ est la fonction définie sur $\mathbb{R}$ par: $f(x)=\Bigg\{ \begin{array}[pos]{c} \frac{1}{b-a}~~~~si~~~~x\in[a;b]\\ 0~~~~si~~~~x\not\in[a;b]\\ \end{array}$.
- $P(a\leq X\leq x)=\displaystyle\int_a^bf(x)dx$ $=\displaystyle\int_a^b\dfrac{1}{b-a}dx$ $=\bigg[\frac{x}{b-a}\bigg]_a^x$ $=\dfrac{x-a}{b-a}$.
- $E(X)=\displaystyle\int_a^bxf(x)dx$ $=\displaystyle\int_a^b\dfrac{x}{b-a}dx$ $=\bigg[\dfrac{x^2}{2(b-a)}\bigg]_a^b$ $=\dfrac{b^2-a^2}{2(b-a)}$
$=\dfrac{(b-a)(a+b)}{2(b-a)}$
Comme $a\not=b$, on a $E(X)=\dfrac{a+b}{2}$.
Propriété.
Soit $X$ une variable aléatoire suivant la loi uniforme sur $[a;b]$ on a:
- Pour tout $x\in[a;b]$ $P(a\leq X\leq x)=\dfrac{x-a}{b-a}$.
- $E(X)=\dfrac{a+b}{2}$.
Loi exponentielle.
Définition .
Une variable aléatoire $X$ suit une loi exponentielle de paramètre $\lambda>0$ lorsque sa densité $f$ est la fonction définie sur $[0;+\infty[$ par: $f(x)=\Bigg\{ \begin{array}[pos]{c} \lambda e^{-\lambda x}~~~~si~~~~x\geq 0\\ 0~~~~si~~~~x < 0\\ \end{array}.$
Par définition on a pour tout $a,b\in[0;+\infty[$ $P(a\leq x\leq b)=\int_a^b\lambda e^{-\lambda x}dx$.- Pour tout $x\in[0;+\infty[$ on a $f(x)\geq 0$.
-
$P(\mathcal{X}\in\mathbb{R})=\displaystyle\lim_{A\to+\infty}\displaystyle\int_{0}^Af(x)dx$ $=\displaystyle\lim_{A\to+\infty}\displaystyle\int_{0}^A\lambda e^{-\lambda x}dx$.
Calulons l'intégrale $\displaystyle\int_{0}^A\lambda e^{-\lambda x}dx$ $=\bigg[-e^{-\lambda x}\bigg]_0^A$ $=1-e^{-\lambda A}$.
Donc comme $\lambda>0$ on a $\displaystyle\lim_{A\to+\infty}1-e^{-\lambda A}=1$.
Proposition.
Soit $X$ une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda$, alors pour tous réels $a$ et $b$ tels que $0\leq a\leq b$ on a: $P(a\leq X\leq b)=e^{-\lambda a}-e^{-\lambda b}.$
$P(X\leq b)=1-e^{-\lambda b}~~~~et~~~~P(X\geq a)=e^{-\lambda a}.$- Pour tous réels $a$ et $b$ tels que $0\leq a\leq b$ on a: $P(a\leq X\leq b)$ $=\displaystyle\int_a^b\lambda e^{-\lambda x}dx$
$=\bigg[-e^{-\lambda x}\bigg]_a^b$ $=e^{-\lambda a}-e^{-\lambda b}$. - $P(X\leq b)=P(0\leq X\leq b)$ $=e^{-\lambda 0}-e^{-\lambda b}$ $=1-e^{-\lambda b}$.
- $P(X\geq a)=1-P(X < a)$ $=1-P(X \leq a)=1-(1-e^{-\lambda a})$ $=e^{-\lambda a}$
Durée de vie sans vieillissement.
$P_{(X\geq t)}(X\geq t+h)=\dfrac{P((X\geq t)\cap(X\geq t+h))}{P(X\geq t)}$ $=\dfrac{P(X\geq t+h)}{P(X\geq t)}$ $=\dfrac{e^{-\lambda (t+h)}}{e^{-\lambda t}}$ $=\dfrac{e^{-\lambda t}\times e^{-\lambda h}}{e^{-\lambda t}}$ $=e^{-\lambda h}=P(X\geq h)$.Proposition.
Soit $X$ un variable aléatoire suivant la loi exponentielle de paramètre $\lambda$, alors pour tout $t\geq 0$ et $h>0$ on a: $P_{(X\geq t)}(X\geq t+h)=P(X\geq h)$.
Soit $g(x)=\lambda xe^{-\lambda x}$ pour tout $x\in[0;+\infty[$. Considérons la fonction $G(x)=(-x-\dfrac{1}{\lambda})e^{-\lambda x}$. Montrons que $G$ est une primitive de $g$ sur $x\in[0;+\infty[$.
$g^{'}(x)=-1\times e^{-\lambda x}+((-x-\dfrac{1}{\lambda})\times (-\lambda)e^{-\lambda x}$ $=\lambda xe^{-\lambda x}=g(x)$.
Calculons $\int_0^A\lambda xe^{-\lambda x} dx$ $=\bigg[(-x-\dfrac{1}{\lambda})e^{-\lambda x}\bigg]_0^A$ $=[(-A-\dfrac{1}{\lambda})e^{-\lambda A}-(-0-\dfrac{1}{\lambda})e^{-\lambda 0}]$ $=\dfrac{1}{\lambda}-(A+\dfrac{1}{\lambda})e^{-\lambda A}$.
$E(X)=\displaystyle\lim_{A\to+\infty}\int_0^A\lambda xe^{-\lambda x} dx$ $=\dfrac{1}{\lambda}-\displaystyle\lim_{A\to+\infty}(A+\dfrac{1}{\lambda})e^{-\lambda A}$.
Calculons $\displaystyle\lim_{A\to+\infty}(A+\dfrac{1}{\lambda})e^{-\lambda A}$, on a $(A+\dfrac{1}{\lambda})e^{-\lambda A}=\dfrac{A}{e^{\lambda A}}+\dfrac{1}{\lambda}e^{-\lambda A}$.
$\Bigg\{ \begin{array}[pos]{c} \displaystyle\lim_{A\to+\infty}\dfrac{A}{e^{\lambda A}}=0\\ \displaystyle\lim_{A\to+\infty}\dfrac{1}{\lambda}e^{-\lambda A}=0\\ \end{array}\Rightarrow \displaystyle\lim_{A\to+\infty}(A+\dfrac{1}{\lambda})e^{-\lambda A}=0$. Donc $\dfrac{1}{\lambda}-\displaystyle\lim_{A\to+\infty}(A+\dfrac{1}{\lambda})e^{-\lambda A}=\dfrac{1}{\lambda}$.Conclusion: $E(X)=\dfrac{1}{\lambda}.$
Définition-proposition.
Soit $X$ une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda$.
On définie l'espérance mathhématique de $X$ comme: $E(X)=\displaystyle\lim_{A\to+\infty}\int_0^A\lambda xe^{-\lambda x} dx$.
On a: $E(X)=\dfrac{1}{\lambda}$.
Définition.
On dit qu'une variable aléatoire $\mathcal{X}$ est continue si il existe une fonction continue sur $\mathbb{R}$ et positive, et telle que pour tout intervalle $I$ de $\mathbb{R}$ on a: $P(\mathcal{X}\in I)=\int_If(x)dx.$ La fonction $f$ est la fonction densité de probabilité de la variable aléatoire $\mathcal{X}$.
Propriété.
Exemple.