Fonctions trigonométriques.
Cosinus, sinus et tangente d'un nombre réel.
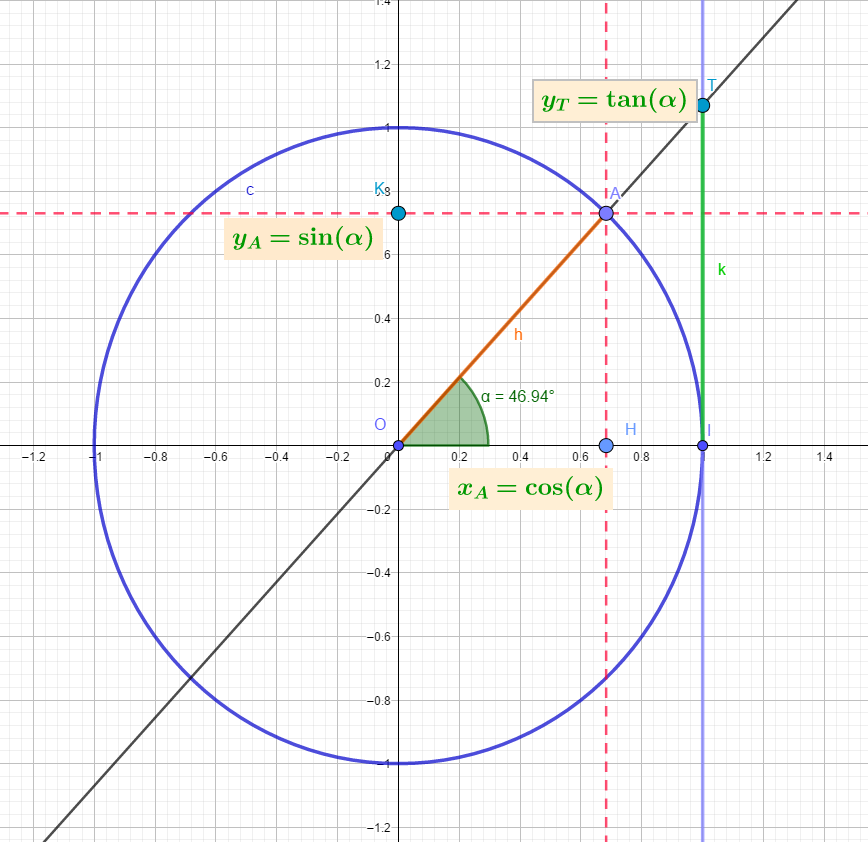
- Soit $\alpha$ un nombre réel et soit $M$ le point du cercle trigonométrique d'abscisse curviligne $\alpha$.
Dans le repère orthonormé $(O,\vec{i},\vec{j})$, le cosinus de $\alpha$, noté $\cos(\alpha)$ est l'abscisse de $M$ et le sinus de $\alpha$ noté $\sin`(\alpha)$
est l'ordonnée de $M$, on a:
$\overrightarrow{OM}=\cos(\alpha)\vec{i}+\sin(\alpha)\vec{j}$. - Par définition, $\tan(\alpha)=\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}$ pour tout $\alpha\not=\frac{\pi}{2}+k\pi$ avec $k\in\mathbb{Z}$.
- $-1\leq\cos x\leq 1$ et $-1\leq\sin x\leq 1$.
- $\cos^2x+\sin^2 x=1$.
- $\cos(x+2k\pi)=\cos x$ et $\sin(x+2k\pi)=\sin x$ pour tout $k\in\mathbb{Z}$.
Fonctions sinus et cosinus.
- La fonction sinus est la fonction définie sur $\mathbb{R}$ qui à tout réel $x$ associe le nombre $\sin(x)$.
- La fonction cosinus est la fonction définie sur $\mathbb{R}$ qui à tout réel $x$ associe le nombre $\cos(x)$.
- Les fonctions sinus et cosinus sont continues sur $\mathbb{R}$.
- Les fonctions sinus et cosinus sont dérivables sur $\mathbb{R}$ et pour tout $x\in\mathbb{R}$ on a:
- $\cos^{'}(x)=-\sin(x)$.
- $\sin^{'}(x)=\cos(x)$.
- Soient $a$ et $b$ deux réels et soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\sin(ax+b)$, alors $f$ est dérivable sur $\mathbb{R}$ et pour tout $x\in\mathbb{R}$ on a: $f'(x)=a\cos(ax+b)$.
- Soient $a$ et $b$ deux réels et soit $g$ la fonction définie sur $\mathbb{R}$ par $g(x)=\cos(ax+b)$, alors $f$ est dérivable sur $\mathbb{R}$ et pour tout $x\in\mathbb{R}$ on a: $g'(x)=-a\sin(ax+b)$.
- $f(x)=\cos(3x+\pi)$ on a $f'(x)=-3\sin(3x+\pi)$.
- $f(x)=\sin(2x-\frac{\pi}{2})$ on a $f'(x)=2\cos(2x-\frac{\pi}{2})$.
Courbes représentatives des fonctions sinus et cosinus.
Propriétés géomètrique des courbes de sinus et cosinus.
- La fonction $f$ est paire si les deux conditions sont vérifiées:
- Pour tout $x\in\mathcal{D}$ le nombre $-x\in\mathcal{D}$.
- Pour tout $x\in\mathcal{D}$, $f(-x)=f(x)$.
- La fonction $f$ est impaire si les deux conditions sont vérifiées:
- Pour tout $x\in\mathcal{D}$ le nombre $-x\in\mathcal{D}$.
- Pour tout $x\in\mathcal{D}$ le nombre $f(-x)=-f(x)$.
- La fonction sinus est impaire.
- La fonction cosinus est paire.
- Si la fonction $f$ est paire, alors la courbe $\mathcal{C}_f$ admet l'axe des ordonnées comme axe de symétrie. On a $\mathcal{C}_f=S_(oy)(\mathcal{C}_f)$.
- Si la fonction $f$ est impaire, alors la courbe $\mathcal{C}_f$ admet l'origine $O$ comme centre de symétrie. On a $\mathcal{C}_f=S_O(\mathcal{C}_f)$.
Fonctions périodiques.
- les fonctions sinus et cosinus sont périodiques, de périodes $2\pi$. En effet on a: $\sin(x+2\pi)=\sin(x)$ et $\cos(x+2\pi)=\cos(x)$.
- La fonction $x\to\sin(2x)$ est périodique, de période $\pi$.En effet on a: $\sin(2(x+\pi))=\sin(2x+2\pi)$ $=\sin(2x)$.
- La fonction $x\to\cos(4x)$ a pour période $\dfrac{\pi}{2}$. En effet on a: $\cos(4(x+\frac{\pi}{2}))=\cos(4x+2\pi)$ $=\cos(4x)$.
Exemples d'inéquations trigonométriques.
Etudier le signe d'une expression trigonométrique.
- <
Dériver une expression trigonométrique.
Etude d'une fonction trigonométrique.
- Pour étudier une fonction trigonométrique sur $\mathbb{R}$.
- On étudie la parité de $f$.
- On étudie la périodicité de $f$.
- On étudie les variations de $f$ sur $I$ l'intervalle réduit obtenu précédemment.
- On trace la courbe représentative de $f$ sur $I$.
- Par des considérations de symétries on complète la courbe représentative de $f$ sur $\mathbb{R}$.
- Montrons que $f$ est paire.
- Pour tout $x\in\mathbb{R}$ le nombre $-x\in\mathbb{R}$.
- Pour tout $x\in\mathbb{R}$ le nombre $f(-x)=\cos(-2x)=\cos(2x)=f(x)$.
Nous déduirons le reste par symétrie axiale par rapport à l'axe $(oy)$. - Montrons que la fonction est $\pi$ périodique.
$f(x+\pi)=\cos(2(x+\pi))=\cos(2x+2\pi)$ $=\cos(x)$.
Conclusion: Comme la fonction est $\pi$ périodique il suffit d'étudier la fonction sur $[0;\pi]$.
- Calcul des variations de $f$. $f'(x)=-2\sin(x)$. Etudions le signe de $f'(x)$.
Pour tout $x\in[0;\pi]$ on a $\sin(x)\geq 0$, donc $f'(x)=-2\sin(x)\leq 0$. Donc la fonction $f$ est décroissante sur $[0;\pi]$.
Définition.
Interprétation Géomètrique du nombre $\tan(\alpha)$.
La droite $(OT)$ a pour vecteur directeur $\overrightarrow{u}\begin{pmatrix}\cos(\alpha)\\\sin(\alpha)\\ \end{pmatrix}$. Donc l'équation cartésienne de la droite $(OT)$ est:$\sin(\alpha)x-cos(\alpha)y=0$. Pour tout $\alpha\not=\frac{\pi}{2}+k\pi$ avec $k\in\mathbb{Z}$ le nombre $\cos(\alpha)\not=0$. Pour tout $\alpha\not=\frac{\pi}{2}+k\pi$ avec $k\in\mathbb{Z}$ la droite $(OT)$ a donc pour équation réduite $y=\tan(\alpha)x$. Le point $T$ a pour abscisse 1, donc $y_T=\tan(\alpha)$.
Proposition.
Définition.
Proposition.
Exemples.
Calculer la fonction dérivée des fonctions $f$ suivantes:
Courbe représentative de $x\to\sin(x)$.
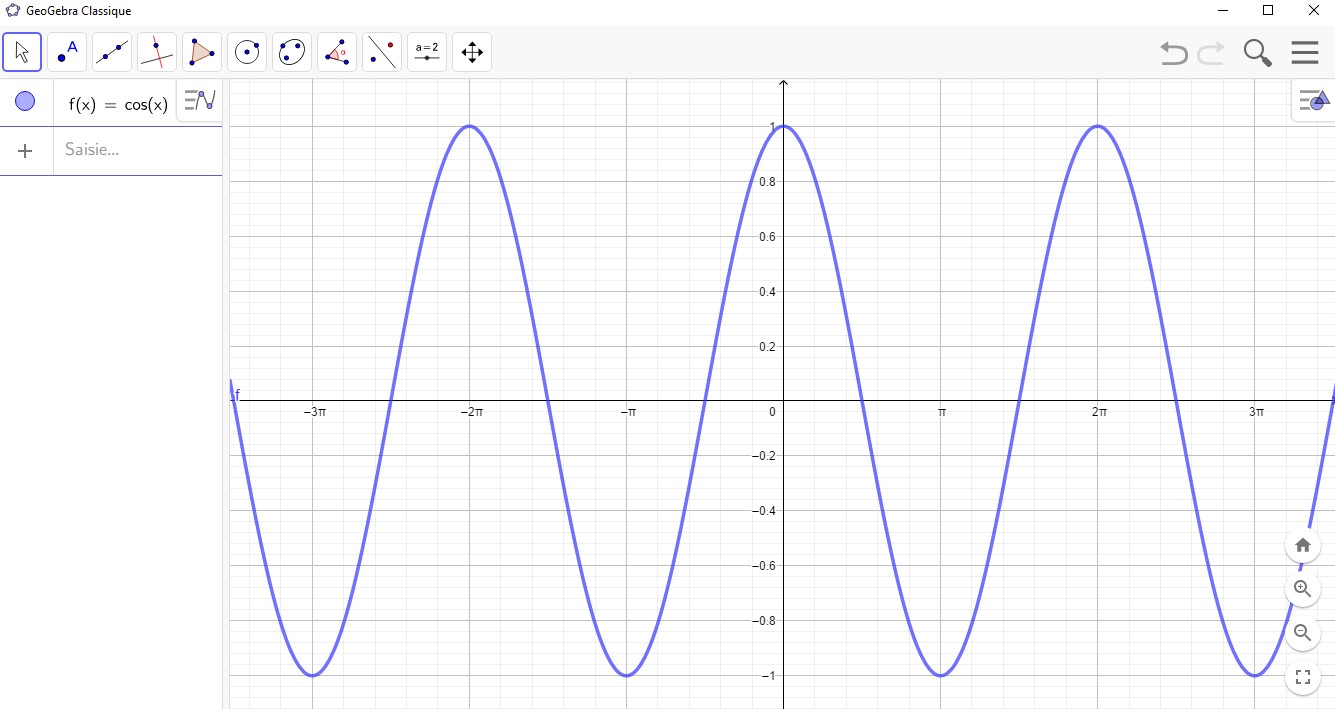
Courbe représentative de $x\to\cos(x)$.
Fonctions paires, fonctions impaires.
Soit $f$ une fonction définie sur une partie $\mathcal{D}$ de $\mathbb{R}$.
Parité des fonctions trigonométriques.
Théorème.
Soit $f$ une fonction représentée par la courbe $\mathcal{C}_f$ dans un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$.
Définition.
Soit $f$ une fonction définie sur $\mathbb{R}$, soit $T$ un nombre réel positif.
On dit que $f$ est une fonction périodique de période $T$ si et seulement si pour tout $x\in\mathbb{R}$ on a:
$f(x+T)=f(x)$.
Exemples.
Exemple1:
Résoudre l'inéquation $\cos(x)\geq\dfrac{\sqrt{2}}{2}$ et $x\in[0,2\pi]$.
Considérons le point $M(\cos(x);\sin(x))$ du cercle trigonométrique.
$\cos(x)\geq\dfrac{\sqrt{2}}{2}$ et $x\in[0,2\pi]$ $\Leftrightarrow$ $x\in[0;\dfrac{\pi}{4}]\cup[\dfrac{7\pi}{4};2\pi]$.
Résolution graphique avec le cercle trigonométrique.
$\cos(x)\geq\dfrac{\sqrt{2}}{2}$ $\Leftrightarrow$ $M$ appartient à l'arc $AA'$ colorié en rouge. Donc $x\in[0;\dfrac{\pi}{4}]\cup[\dfrac{7\pi}{4};2\pi]$. Donc nous avons l'équivalence:$\cos(x)\geq\dfrac{\sqrt{2}}{2}$ et $x\in[0,2\pi]$ $\Leftrightarrow$ $x\in[0;\dfrac{\pi}{4}]\cup[\dfrac{7\pi}{4};2\pi]$.
Exemple2:
Résoudre l'inéquation $\sin(x) < \dfrac{\sqrt{3}}{2}$ et $x\in[-\pi,2\pi[$.
Considérons le point $M(\cos(x);\sin(x))$ du cercle trigonométrique.
$\sin(x) < \dfrac{\sqrt{3}}{2}$ et $x\in[-\pi,2\pi[$ $\Leftrightarrow$ $x\in[-\pi;\dfrac{\pi}{3}[\cup]\dfrac{2\pi}{3};2\pi[$.
Résolution graphique avec le cercle trigonométrique.
$\sin(x) < \dfrac{\sqrt{3}}{2}$ $\Leftrightarrow$ $M$ appartient à l'arc $AA'$ colorié en rouge. Donc $x\in[-\pi;\dfrac{\pi}{3}[\cup]\dfrac{2\pi}{3};2\pi[$. Donc nous avons l'équivalence:$\sin(x) < \dfrac{\sqrt{3}}{2}$ et $x\in[-\pi,2\pi[$ $\Leftrightarrow$ $x\in[-\pi;\dfrac{\pi}{3}[\cup]\dfrac{2\pi}{3};2\pi[$.
Méthode.
Comme pour les expressions algébriques, pour étudier facilement le signe d'une expression trigonométrique, il faut la mettre si possible sous la forme de facteurs de la forme $a\cos(x)+b$ ou $a'\sin(x)+b'$.
Exemple.
Etudions le signe de $f(x)=\sin(x)\times\cos(x)$ sur l'intervalle $[-\pi;\pi]$.
$\cos(x)\geq 0$ et $x\in[-\pi;\pi]$ $\Leftrightarrow$ $x\in[-\dfrac{\pi}{2};\dfrac{\pi}{2}]$.
$\sin(x)\geq 0$ et $x\in[-\pi;\pi]$ $\Leftrightarrow$ $x\in[0;\pi]$.
Ces deux équivalence permettent de remplir les lignes du tableaux de signes ci-contre.
Exemple.
Soit $f$ la fonction définie sur $[-\dfrac{\pi}{2};\dfrac{\pi}{2}]$ par $f(x)=\dfrac{\sin(x)}{\cos(x)+1}$.
Calculer $f'(x)$.
$f(x)=\dfrac{u(x)}{v(x)}$ avec $u(x)=\sin(x)$ et $v(x)=\cos(x)+1$, on a $u'(x)=\cos(x)$ et $v'(x)=-\sin(x)$.
Donc $f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{v(x)^2}$ $=\dfrac{\cos(x)(\cos(x)+1)-\sin(x)(-\sin(x))}{(\cos(x)+1)^2}$ $=\dfrac{\cos^2(x)+\cos(x)+\sin^2(x)}{(\cos(x)+1)^2}$ $=\dfrac{1+\cos(x)}{(1+\cos(x))^2}$ $=\dfrac{1}{1+\cos(x)}$.
Donc $f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{v(x)^2}$ $=\dfrac{\cos(x)(\cos(x)+1)-\sin(x)(-\sin(x))}{(\cos(x)+1)^2}$ $=\dfrac{\cos^2(x)+\cos(x)+\sin^2(x)}{(\cos(x)+1)^2}$ $=\dfrac{1+\cos(x)}{(1+\cos(x))^2}$ $=\dfrac{1}{1+\cos(x)}$.
Une limite importante à connaître!
$\displaystyle\lim_{x\to 0}\frac{\sin(x)}{x}=1.$Méthode.
Exercice.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\cos(2x)$. Etudier la fonction $f$.