Nombres premiers.
Définition et propriétés des nombres premiers.
- Un entier naturel distinct de $1$ $p\not=1$ est premier s'il admet exactement deux diviseurs (dans $\mathbb{N}$), 1 et lui-même.
- un entier distinct de 1 et non premier est dit composé.
- Par exemple $8$ n'est pas premier il est composé.
- Voici la liste des nombres premiers inférieur à 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
- Tout entier naturel $n\geq 2$ admet au moins un diviseur premier.
- Si $n\geq 2$ et non premier alors $n$ admet un diviseur premier $p$ tel que $p\leq\sqrt{n}$.
- Montrons que le plus petit diviseur de $n$ compris entre 2 et $n$ est premier.
Soit $p$ le plus petit diviseur de $n$ compris entre 2 et $n$, raisonnons par l'absurde. Supposons que $p$ n'est pas premier, donc $p=a\times b$ avec donc par exemple $a$ un diviseur de $n$, et $1 < a < p$, ce qui est absurde puisque $p$ est le plus petit des diviseurs de $n$. Donc $p$ est premier. - D'après la propriété précédente, le plus petit diviseur de $n$ compris entre 2 et $n$ est premier.Notons ce nombre $d$ et $d < n$, puique $n$ n'est pas premier par hypothèse.
On peut écrire $n=d\times d'$ avec $2\leq d\leq d'\leq n$, car $n$ est le plus petit des diviseurs de $n$.
Nous en deéduisons que $d\times d\leq d\times d'=n$, donc $d^2\leq n$, c'est à dire $d\leq\sqrt{n}$. Utilisation d'un algorithme.
Rechercher la liste des nombres premiers inférieurs ou égaux à un entier naturel $N$.
Proposition
- Soient $p$ un nombre premier et $n$ un entier naturel. alors $p$ divise $n$ ou $p$ est premier avec $n$.
En particulier, un nombre premier $p$ est premier avec tout nombre naturels qui lui est strictement inférieur. - Si $p$ est un nombre premier si il divise le produit $a\times b$ alors $p$ divise $a$ ou $p$ divise $b$.
- L'ensemble des nombres premiers est infini.
- Montrons qu'il existe une infinité de nombres premiers.
Raisonnons par l'absurde. Supposons qu'il existe un nombre fini d'entiers premiers. Soit $p$ le plus grand d'entre-eux et soit $N$ le produit de tous ces nombres premiers.
Donc par exemple pour fixer les idées prenons $N=2\times 3\times...\times p$ Considérons l'entier $N+1$.
Puisque $N+1=2\times 3\times 5\times...\times p+1$, donc le reste de la division euclidienne de $N$ par $2,3,5,...,p$ est égal à $1$. Donc $N+1$ n'est pas divisible par $2,3,5,...,p$.
Nous remarquons que $p\leq N+1$, donc d'après le test de primalité, $N+1$ est un nombre premier, ce qui est absurde. Donc l'ensemble des nombres premiers est infini.
- Soient $p$ un nombre premier et $n$ un entier naturel. alors $p$ divise $n$ ou $p$ est premier avec $n$.
Décomposition en facteurs premiers.
- Existence: Tout entier supérieur ou égal à deux est premier ou est un produit de nombres premiers.
- Unicité: Cette décomposition est unique, elle porte le nom de décomposition en facteurs premiers.
- Raisonnons par l'absurde.
Pour simplifier notons $\mathcal{P}$="Tout entier supérieur ou égal à deux est premier ou est un produit de nombres premiers".
La propriété est vraie pour les premiers entiers 2;3; $4=2\times 2;5$; $6=2\times 3$....
Supposons qu'elle ne soit pas vraie pour un entier $r$ particulier, nous pouvons choisir cet entier $r$ pour qu'il soit le plus petit des entiers à mettre en défaut la propriété à démontrer. Donc le nombre entier $r$ est ni premier ni produit de nombres premiers. Mais nous savons quil existe un entier $p$ premier avec $p\leq\sqrt{n} < n$.
Donc $r=pd$ où $1 < d < r$.Donc comme $r$ est le plus petit entier ne vérifiant pas la propriéte.
Finalement nous voyons qu'on peut créer une suite d'entiers naturels strictement décroissante. cette suite est nécessairement finie et son dernier terme est premier. En regroupant les facteurs premiers identiques on obtient une écriture de n.
$n= p_1^{\alpha_1}\times p_2^{\alpha_2}\times...\times p_s^{\alpha_s}$ où $p_1$, $p_2$,..., $p_s$ sont des nombres premiers tous distincts deux à deux et $\alpha_i$ sont des entiers positifs ou nuls. - Démontrons l'unicité. Pour cela nous allons faire un raisonnement par l'absurde dans une récurrence.
Considérons la propriété $\mathcal{P}_n$="la décomposition en nombres premiers est unique pour l' entier $n\geq 2$".
Le but de la démonstration est de démontrer que pour tout $n\geq 2$ la propriété $\mathcal{P}_n$ est vraie.- Initialisation: si $n=2$ la propriété est $\mathcal{P}_2$ est vraie.
- Transmission: Supposons qu'il existe un entier naturel $p\geq 2$ pour tout entier $q\leq p$ la propriété $\mathcal{P}_q$ est vraie.
Vous devons montrer que $\mathcal{P}_{p+1}$ est encore vraie, c'est pour cela cela supposons que le nombre $n+1$ admette deux décomposition distnctes en produit de facteur premiers.
C'est à dire $n+1=p_1\times p_2\times ...\times p_r=q_1\times q_2\times ...\times q_s$.
Si $p_1$ est premier avec $q_i$ pour tout $1\leq i\leq s$, alors d'après le corollaire du théorème de Gauss $p_1$ est premier avec $q_1\times q_2\times ...\times q_s$. Or $p_1$ divise $q_1\times q_2\times ...\times q_s$, d'ou la contradiction.
Il existe donc un entier $i$ tel que $p_1=q_i$.
Le nombre $n_1=\dfrac{n+1}{p_1}$ admettrait donc deux décomposition distinctes:
$n_1= p_2\times ...\times p_r=q_1\times q_2\times ...\times q_{i-1}\times q_{i+1}\times ...\times q_s$ ce qui contrdit aussi l'hypothèse de récurrence car $n_1 < n$ car $p_2\geq 2$.
On en déduit que $n+1$ admet une décomposition unique. - Pour tout $n\geq 2$ la propriété $\mathcal{P}_n$ est vraie, ce qui veut dire exactement que la décomposition de tout nombre entier $n\geq 2$ en nombre premiers est unique.
Applications de la décomposition en facteurs premiers.
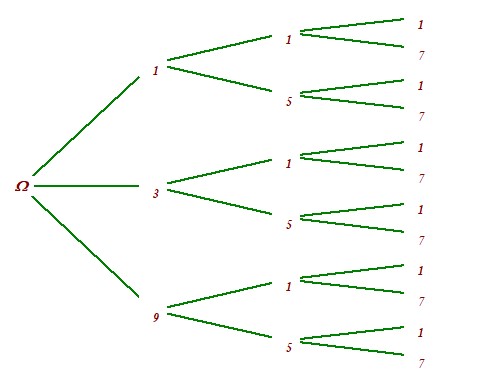
- Nous avons $315=3^2\times 5\times 7$. En formant l'arbre ci-contre, nous pouvons en déduire que:
Diviseurs=$\{1;3;5;7;9;15;21;35;45;63;105;315\}$, le nombre de diviseurs est 12. Vérifions la formule $N=(2+1)\times (1+1)\times (1+1)=12$. Ca marche! - Autre exemple: $13000=2^3\times 5^3\times 13$.
Nombre de diviseurs=$(3+1)\times (3+1)\times (1+1)=32$.
Définition.
Exemples.
Propriétés.
Si un entier $n$ n'est divisible par aucun nombre premier inférieur à sa racine carrée, il est alors premier.
Exemple.
Le nombre 173 est-il premier?
$\sqrt{173}\approx13,153$.
La liste des diviseurs premiers inférieur inférieur ou égal à $\sqrt{173}$ est 2;3;5;7;11;13.
Aucun de ces nombres divisent $173$, donc 173 est un nombre premier.
Proposition.
Proposition.
Soient $a$ et $b$ deux entiers supérieurs ou égaux à 1.
Si $a=p_1^{\alpha_1}\times p_2^{\alpha_2}\times...\times p_s^{\alpha_s}$ et $b=p_1^{\beta_1}\times p_2^{\beta_2}\times...\times p_s^{\beta_s}$
ou $p_1$, $p_2$,..., $p_s$ sont des nombres premiers tous distincts deux à deux et $\alpha_i$ et $\beta_i$
sont des entiers positifs ou nuls, alors $b$ divise $a$ si et seulement si, pout tout $1\leq i\leq s$ on a $0\leq \beta_i\leq\alpha_i$.
Calcul du PGCD de deux nombres entiers.
Soint $a=p_1^{\alpha_1}\times p_2^{\alpha_2}\times...\times p_s^{\alpha_s}$ et $b=p_1^{\beta_1}\times p_2^{\beta_2}\times...\times p_s^{\beta_s}$, ou $p_1$, $p_2$,..., $p_s$ sont des nombres premiers tous distincts deux à deux et $\alpha_i$ et $\beta_i$ sont des entiers positifs ou nuls.
Alors
$PGCD(a,b)=p_1^{\gamma_1}\times p_2^{\gamma_2}\times...\times p_s^{\gamma_s}$
avec pour tout $1\leq i\leq s$ les nombres $\gamma_i=min(\alpha_i,\beta_i)$.
Dénombrement des diviseurs d'un entier.
Soit $a$ un entier naturel, avec $a=p_1^{\alpha_1}\times p_2^{\alpha_2}\times...\times p_s^{\alpha_s}$ sa décomposition en nombre premiers.
Le nombre de diviseurs positifs de $a$ est égal à $(\alpha_1+1)\times (\alpha_2+1)\times ....\times (\alpha_s+1)$.
Exemple.
Rechercher les diviseurs d'un nombre ($N\leq 100000$)