Equations de sphères.
Relations métriques dans un triangle quelconque.
- si $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d>0$, alors $\mathcal{S}$ est la sphère de centre $I(-\dfrac{a}{2};-\dfrac{b}{2};-\dfrac{c}{2})$ et de rayon $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d>0$.
- si $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d=0$, alors $\mathcal{S}$ est restreint au point $I(-\dfrac{a}{2};-\dfrac{b}{2};-\dfrac{c}{2})$.
- si $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d < 0$, alors $\mathcal{S}$ est l'ensemble vide.
- Premier cas: $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d>0$.
Posons $I(-\dfrac{a}{2};-\dfrac{b}{2};-\dfrac{c}{2})$ et $r=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d}$, on a donc:
$\bigg(x+\dfrac{a}{2}\bigg)^2+\bigg(y+\dfrac{b}{2}\bigg)^2+\bigg(z+\dfrac{c}{2}\bigg)^2=\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d$ $\Leftrightarrow$ $IM^2=r^2$ $\Leftrightarrow$ $M$ appartient à la sphère de centre $I$ et de rayon $r$.
$\mathcal{S}$ est la sphère de centre $I(-\dfrac{a}{2};-\dfrac{b}{2};-\dfrac{c}{2})$ et de rayon $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d>0$. - Deuxième cas: $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d=0$.
$\bigg(x+\dfrac{a}{2}\bigg)^2+\bigg(y+\dfrac{b}{2}\bigg)^2+\bigg(z+\dfrac{c}{2}\bigg)^2=\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d$ $\Leftrightarrow$ $IM^2=0$ $\Leftrightarrow$ $IM=0$ $\Leftrightarrow$ $M$ et $I$ sont confondus.
$\mathcal{S}$ est restreint au point $I(-\dfrac{a}{2};-\dfrac{b}{2};-\dfrac{c}{2})$. - Troisième cas: $\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d < 0$.
L'équation $\bigg(x+\dfrac{a}{2}\bigg)^2+\bigg(y+\dfrac{b}{2}\bigg)^2+\bigg(z+\dfrac{c}{2}\bigg)^2=\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d$ est impossible, donc $\mathcal{S}$ est l'ensemble vide. - $x^2+y^2+z^2-2x+y-4z+1=0$.
- $x^2+y^2+z^2-2x+8y+5=0$.
- $2x^2+2y^2+2z^2-4x-8y+8z+20=0$.
- $x^2+y^2+z^2-2x+y-4z+1=0$ $\Leftrightarrow$ $(x-1)^2-1+(y+\dfrac{1}{2})^2-\dfrac{1}{4}+(z-2)^2-4+1=0$
Donc $x^2+y^2+z^2-2x+y-4z+1=0$ $\Leftrightarrow$ $(x-1)^2+(y-\dfrac{1}{2})^2+(z-2)^2=\dfrac{17}{4}$.
Si on pose $I(1;-\dfrac{1}{2};2)$ et $r=\dfrac{\sqrt{17}}{2}$, on a l'équivalence:
$M(x;y;z)$, vérifie $x^2+y^2+z^2-2x+y-4z+1=0$ $\Leftrightarrow$ $IM=r$.
On en déduit que l'ensemble des points $M(x;y;z)$, vérifiant $x^2+y^2+z^2-2x+y-4z+1=0$ est la sphère de centre $I(1;-\dfrac{1}{2};2)$ et de rayon $r=\dfrac{\sqrt{17}}{2}$. - $x^2+y^2+z^2-2x+8y+5=0$ $\Leftrightarrow$ $(x-1)^2-1+(y+4)^2-16+z^2+5=0$
Donc $x^2+y^2+z^2-2x+8y+5=0$ $\Leftrightarrow$ $(x-1)^2+(y+4)^2+z^2=12$.
Si on pose $I(1;-4;0)$ et $r=\sqrt{12}=2\sqrt{3}$, on a l'équivalence:
$M(x;y;z)$, vérifie $x^2+y^2+z^2-2x+8y+5=0$ $\Leftrightarrow$ $IM=r$.
On en déduit que l'ensemble des points $M(x;y;z)$, vérifiant $x^2+y^2+z^2-2x+8y+5=0$ est la sphère de centre $I(1;-4;0)$ et de rayon $r=2\sqrt{3}$. - En divisant par deux, on obtient:
$2x^2+2y^2+2z^2-4x-8y+8z+20=0$ $\Leftrightarrow$ $x^2+y^2+z^2-2x-4y+4z+10=0$.
$x^2+y^2+z^2-2x-4y+4z+10=0$ $\Leftrightarrow$ $(x-1)^2-1+(y-2)^2-4+(z+2)^2-4+10=0$.
$x^2+y^2+z^2-2x-4y+4z+10=0$ $\Leftrightarrow$ $(x-1)^2+(y-2)^2+(z+2)^2=-1$.
L'équation $(x-1)^2+(y-2)^2+(z+2)^2=-1$ est impossible. Intersection d'une sphère et d'une droite.
Deux points d'intersections.
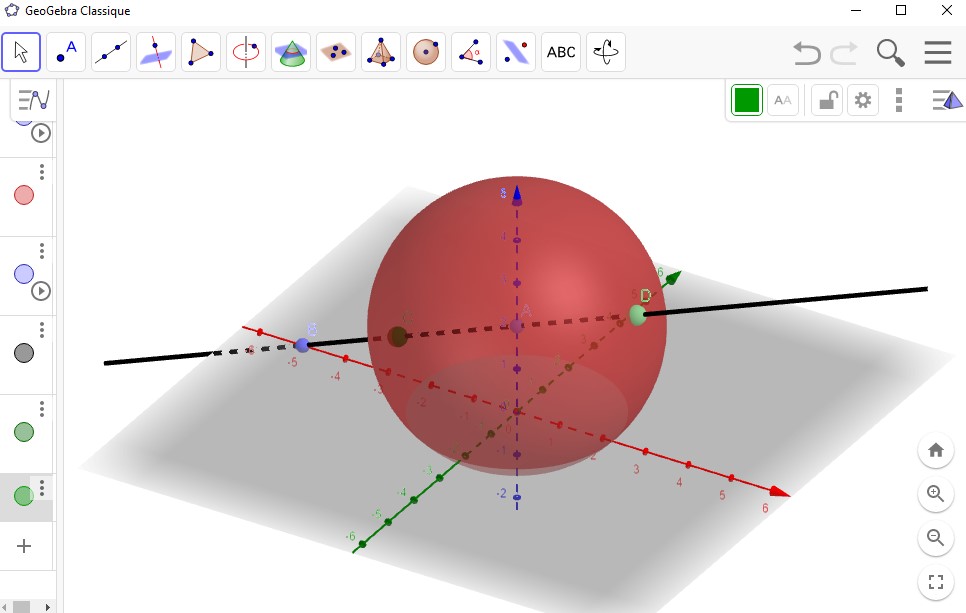
Dans un repère orthonormé déterminer l'intersection entre la sphère $\mathcal{S}$ et la droite $(d)$.
- $(d):\Bigg\{\begin{array}[pos]{c}x=6-k \\y=-4+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-21=0$.
Un point d'intersection.
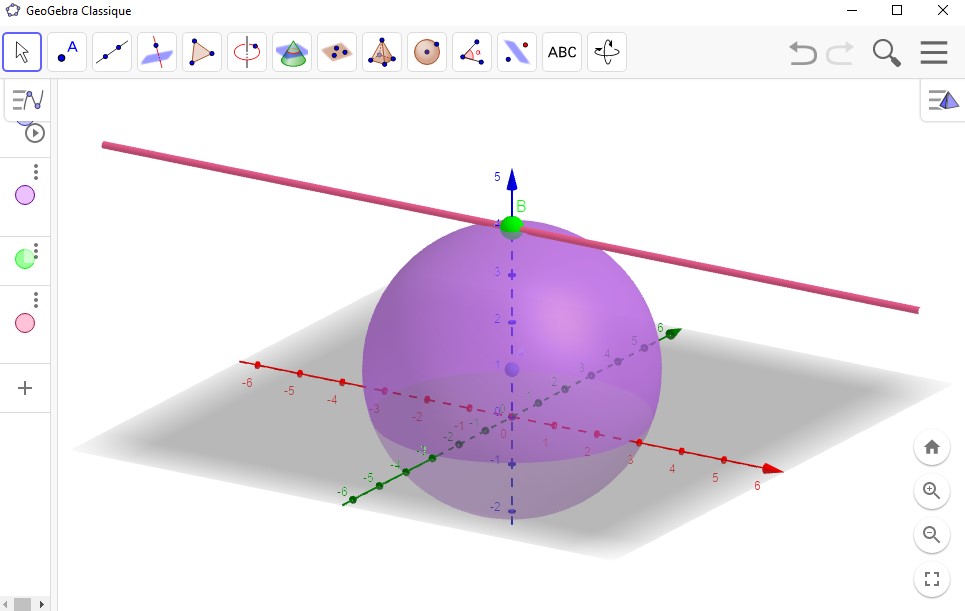
Dans un repère orthonormédéterminer l'intersection entre la sphère $\mathcal{S}$ et la droite $(d)$.
- $(d):\Bigg\{\begin{array}[pos]{c}x=t \\y=t\\z=3 \\ \end{array}$ avec $t\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-2y-2z-1=0$.
Aucun point d'intersection.

Dans un repère orthonormédéterminer l'intersection entre la sphère $\mathcal{S}$ et la droite $(d)$.
- $(d):\Bigg\{\begin{array}[pos]{c}x=3+k \\y=1+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-y-z-10=0$.
- $(d):\Bigg\{\begin{array}[pos]{c}x=6-k \\y=-4+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-21=0$.
$(6-k)^2+(-4+2k)^2+(1+k)^2-2(6-k)-7=0$ $\Leftrightarrow$ $k^2-12k+36+4k^2-16k+16+k^2+2k+1-12+2k-21=0$ $\Leftrightarrow$ $6k^2-24k+20=0$ $\Leftrightarrow$ $3k^2-12k+10=0$.
Résolvons l'équation $3k^2-12k+10=0$.
$\Delta=(-12)^2-4\times 3\times 10=24>0$, donc il existe deux solution réelles distinctes;
$k_0=\dfrac{12-\sqrt{24}}{6}=2-\dfrac{\sqrt{6}}{3}$ et $k_1=\dfrac{12+\sqrt{24}}{6}=2+\dfrac{\sqrt{6}}{3}$.
L'ensemble $\mathcal{S}\cap (d)$ est constitué de deux points $A$ et $B$.
Si $k=k_0=2-\dfrac{\sqrt{6}}{3}$ $\Rightarrow$ $\Bigg\{\begin{array}[pos]{c}x_A=6-k_0 \\y_A=-4+2k_0\\z_A=1+k_0 \\ \end{array}$
Si $k=k_1=2+\dfrac{\sqrt{6}}{3}$ $\Rightarrow$ $\Bigg\{\begin{array}[pos]{c}x_B=6-k_1 \\y_B=-4+2k_1\\z_B=1+k_1 \\ \end{array}$- $(d):\Bigg\{\begin{array}[pos]{c}x=t \\y=t\\z=3 \\ \end{array}$ avec $t\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-2y-2z-1=0$.
Il existe qu'une solution $t=1$, donc l'ensemble $\mathcal{S}\cap (d)$ est constitué d'un seul points $A$, on dit que la droite $(d)$ est tangente à la sphère $\mathcal{S}$.
Si $t=1$ $\Rightarrow$ $\Bigg\{\begin{array}[pos]{c}x_A=1 \\y_A=1\\z_A=3 \\ \end{array}$.- $(d):\Bigg\{\begin{array}[pos]{c}x=3+k \\y=1+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.
- $\mathcal{S}:x^2+y^2+z^2-2x-y-z+20=0$.
$(3+k)^2+(1+2k)^2+(1+k)^2-2(3+k)-(1+2k)-(1+k)-2=0$ $\Leftrightarrow$ $k^2+6k+9+4k^2+4k+1+k^2+2k+1-6-2k-1-2k-1-k+20=0$ $\Leftrightarrow$ $6k^2+9k+23=0$.
Résolvons l'équation $6k^2+9k+23=0$.
$\Delta=9^2-4\times 6\times 23=-471 < 0$, donc l'équation ne possède pas de solution réelle, donc $\mathcal{S}\cap (d)=\emptyset$.
Théorème.
Dans un repère orthonormé, soit un point $I(x_0;y_0;z_0)$ et soit un réel $r$ strictement positif $r>0$.
La sphère $\mathcal{S}$ de centre $I$ et de rayon $r$ est l'ensemble des points $M(x;y)$ du plan tel que $IM=r$.
La sphère $\mathcal{S}$ de centre $I$ et de rayon $r$ admet pour équation cartésienne l'équation:
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=r^2.$
$\mathcal{S}:x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+x_0^2+y_0^2+z_0^2-r^2=0$.

$M(x;y;z)\in\mathcal{S}$ $\Leftrightarrow$ $IM=r$ $\Leftrightarrow$ $IM^2=r^2$.
$M(x;y;z)\in\mathcal{S}$ $\Leftrightarrow$ $(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=r^2$
$\Leftrightarrow$ $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+x_0^2+y_0^2+z_0^2=r^2$
$\Leftrightarrow$ $x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+x_0^2+y_0^2+z_0^2-r^2=0$.
Conclusion: $\mathcal{S}:x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+x_0^2+y_0^2+z_0^2-r^2=0$.
Exercice.
Donner l'équation de la sphère $\mathcal{S}$ de centre $\Omega(-1;2;-3)$ et de rayon $3$.
$M(x;y;z)\in\mathcal{S}$ $\Leftrightarrow$ $\Omega M=3$ $\Leftrightarrow$ $\Omega M^2=9$.
$M(x;y;z)\in\mathcal{S}$ $\Leftrightarrow$ $(x+1)^2+(y-2)^2+(z+3)^2=9$
$\Leftrightarrow$ $x^2+y^2+z^2+2x-4y+6z+1+4+9=9$
$\Leftrightarrow$ $x^2+y^2+z^2+2x-4y+6z+5=0$.
Conclusion: $\mathcal{S}:x^2+y^2+z^2+2x-4y+6z+5=0$.
Réciproque du théorème.
Dans un repère orthonormé, l'ensemble $\mathcal{S}$ des points $M(x;y;z)$ vérifiant une équation de la forme: $x^2+y^2+z^2+ax+by+cz+d=0,$
Dans un repère orthonormé, considérons l'ensemble $\mathcal{S}$ des points $M(x;y;z)$ vérifiant une équation:
$x^2+y^2+z^2+ax+by+cz+d=0$
En utilisant la même méthode pour déterminer la forme canonique d'un trinôme du second degré.
$x^2+y^2+z^2+ax+by+cz+d=0$ $\Leftrightarrow$ $(x^2+ax)$+$(y^2+by)$+$(z^2+cz)$+d=0
$\Leftrightarrow$ $\bigg(x+\dfrac{a}{2}\bigg)^2-\dfrac{a^2}{4}$+$\bigg(y+\dfrac{b}{2}\bigg)^2-\dfrac{b^2}{4}$+$\bigg(z+\dfrac{c}{2}\bigg)^2-\dfrac{c^2}{4}$+d=0.
Donc on a: $x^2+y^2+z^2+ax+by+cz+d=0$ $\Leftrightarrow$ $\bigg(x+\dfrac{a}{2}\bigg)^2+\bigg(y+\dfrac{b}{2}\bigg)^2+\bigg(z+\dfrac{c}{2}\bigg)^2-\dfrac{a^2}{4}-\dfrac{b^2}{4}-\dfrac{c^2}{4}+d=0$
$\Leftrightarrow$ $\bigg(x+\dfrac{a}{2}\bigg)^2+\bigg(y+\dfrac{b}{2}\bigg)^2+\bigg(z+\dfrac{c}{2}\bigg)^2=\dfrac{a^2}{4}+\dfrac{b^2}{4}+\dfrac{c^2}{4}-d$
Trois cas se posent donc:
Exercice.
Dans un repère orthonormé, on donne les équations suivantes, pour chacune de ces équations, reconnaitre l'ensemble.
Théorème.
La sphère de diamètre $[AB]$ est l'ensemble des points $M$ tels que $\overrightarrow{MA}.\overrightarrow{MB}=0$.
Considérons l'ensemble $\mathcal{E}$ des points $M$ de l'espace tels que $\overrightarrow{MA}.\overrightarrow{MB}=0$, montrons que $\mathcal{E}$
est la sphère de diamètre $[AB]$.
$M\begin{pmatrix}x\\y\\z\\ \end{pmatrix}\in\mathcal{S}$ $\Leftrightarrow$ $\overrightarrow{MA}.\overrightarrow{MB}=0$ $\Leftrightarrow$ $\overrightarrow{AM}.\overrightarrow{BM}=0$
$\overrightarrow{AM}\begin{pmatrix}x-x_A\\y-y_A\\z-z_A\\ \end{pmatrix}$ et $\overrightarrow{BM}\begin{pmatrix}x-x_B\\y-y_B\\z-z_B\\ \end{pmatrix}$, donc on a:
$\overrightarrow{AM}.\overrightarrow{BM}=0$ $\Leftrightarrow$ $(x-x_A)(x-x_B)+(y-y_A)(y-y_B)+(z-z_A)(z-z_B)=0$
$\Leftrightarrow$ $x^2+y^2-(x_A+x_B)x-(y_A+y_B)y-(z_A+z_B)z+x_Ax_B+y_Ay_B+z_Az_B=0$
$\Leftrightarrow$ $x^2+y^2-(x_A+x_B)x-(y_A+y_B)y+x_Ax_B+y_Ay_B+z_Az_B=0$
$\Leftrightarrow$
$\bigg(x-\dfrac{x_A+x_B}{2}\bigg)^2+\bigg(y-\dfrac{y_A+y_B}{2}\bigg)^2+\bigg(z-\dfrac{z_A+z_B}{2}\bigg)^2-\bigg(\dfrac{x_A+x_B}{2}\bigg)^2-\bigg(\dfrac{y_A+y_B}{2}\bigg)^2-\bigg(\dfrac{z_A+z_B}{2}\bigg)^2+x_Ax_B+y_Ay_B+z_Az_B=0$
$\Leftrightarrow$ $\bigg(x-\dfrac{x_A+x_B}{2}\bigg)^2+\bigg(y-\dfrac{y_A+y_B}{2}\bigg)^2+\bigg(z-\dfrac{z_A+z_B}{2}\bigg)^2-\bigg(\dfrac{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}{4}\bigg)=0$
$\Leftrightarrow$ $\bigg(x-\dfrac{x_A+x_B}{2}\bigg)^2+\bigg(y-\dfrac{y_A+y_B}{2}\bigg)^2+\bigg(z-\dfrac{z_A+z_B}{2}\bigg)^2=\dfrac{AB^2}{4}=\bigg(\dfrac{AB}{2}\bigg)^2$
Donc Le point $M$ appartient au cercle de centre $I\bigg(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2};\dfrac{z_A+z_B}{2}\bigg)$ et de rayon $\dfrac{AB}{2}$, on remarque que $I$ est le milieu
du segment $[AB]$.
Donc le point $M$ appartient au cercle de diamètre $[AB]$.