Intégrale d'une fonction continue sur un intervalle.
Intégrale d'une fonction en escalier.
- Soit $f$ une fonction définie sur $[a;b]$ telle que pour tout $x\in]a;b[$; $f(x)=c$.
Par définition l'intégrale de $f$ sur l'intervalle $[a;b]$ est le nombre réel: $I(f)=(b-a)c.$ - Soit $f$ une fonction en escalier, et soit $x_0;x_1;x_2;...;x_{n-1};x_n$ n+1 nombres réels strictement rangés par ordre croissant
tels que pour $0\leq i\leq n-1$ $f(x)=c_i$ pour tout $x\in]x_i;x_{i+1}[$.
Par définition l'intégrale de $f$ sur l'intervalle $[a;b]$ est le nombre réel:
$I(f)=\sum_{i=0}^{n-1}(x_{i+1}-x_i)c_i$ $=(x_1-x_0)c_0+(x_2-x_1)c_1+$ $...+(x_n-x_{n-1})c_{n-1}.$ Intégrale d'une fonction continue sur un intervalle borné.
Propriété admise en terminale.
Soit $f$ une fonction continue, il existe deux suites de fonctions en escalier $(g_n)$ et $(h_n)$ telles que pour tout $n\in\mathbb{N}$ et tout $x\in[a;b]$, on a $g_n(x)\leq f(x)\leq h_n(x)$. De plus on a: $\displaystyle\lim_{n\to+\infty}I(g_n)=\displaystyle\lim_{n\to+\infty}I(h_n)=l.$
De plus si il existe deux autres suites de fonctions $(g'_n)$ et $(h'_n)$ en escalier encadrant $f$, on démontre aussi que: $\displaystyle\lim_{n\to+\infty}I(g'_n)=\displaystyle\lim_{n\to+\infty}I(h'_n)=l.$Définition.
La limite $l$ est l'intégrale de $f$ sur $[a;b]$ $(a\leq b)$. On note: $l=\displaystyle\int_a^bf(t)dt$.
Aire sous la courbe d'une fonction positive.
Approximation d'une intégrale.
- La somme des aires des rectangles verts est égale à $S_{inf}=\dfrac{1}{10}\bigg(f(0.1)+f(0.2)+...f(0.9)+f(1)\bigg)$.
- La somme des aires des rectangles rouges est égale à $S_{sup}=\dfrac{1}{10}\bigg(f(0)+f(0.1)+...f(0.8)+f(0.9)\bigg)$.
Calcul d'une intégrale à l'aide des primitives.
Théoréme fondamental(admis en terminale):
- Soit $f$ une fonction continue sur un intervalle $I$, et soit $a$ un réel de $I$.
La fonction définie sur $I$ par $F(x)=\displaystyle\int_a^xf(t)dt$ est l'unique primitive de $f$ sur $I$ telle que $F(a)=0$. - Soit $f$ une fonction continue sur un intervalle $I$, $F$ est une primitive quelconque de $f$ sur $I$, soit $a$ et $b$ deux réels de $I$, alors on a:
$\displaystyle\int_a^bf(t)dt=F(b)-F(a)$.
On écrit par commodité la différence $F(b)-F(a)$ sous la forme $\bigg[f(t)\bigg]_a^b$, on a donc:
$\displaystyle\int_a^bf(t)dt=F(b)-F(a)=\bigg[F(t)\bigg]_a^b.$
Exemple.
Calculons l'intégrale $\displaystyle\int_0^1\dfrac{e^x}{e^x+1}dx$.
Recherchons une primitive de $f(x)=\dfrac{e^x}{e^x+1}$ définie sur $\mathbb{R}$. On remarque que cette fonction est de la forme $\dfrac{u'}{u}$.
En effet pour tout $x\in\mathbb{R}$, on a $f(x)=\dfrac{u'(x)}{u(x)}$, avec $u(x)=e^x+1$.
Donc la fonc $F(x)=\ln(e^x+1)$ est une primitive de $f$ sur $\mathbb{R}$, donc $\displaystyle\int_0^1\dfrac{e^x}{e^x+1}dx=\bigg[\ln(e^x+1)\bigg]_0^1$ $=\ln(e+1)-ln(2)=ln\bigg(\dfrac{e+1}{2}\bigg)$.Exercices.
Calculer les intégrales suivantes et donner une interprétation graphique.
- $\displaystyle\int_0^1(x^3+x)dx$.
- $\displaystyle\int_0^{\frac{\pi}{2}}\sin(u)du$.
- $\displaystyle\int_1^{e^2}\dfrac{1}{x}dx$.
- $\displaystyle\int_0^1e^tdt$.
- $\displaystyle\int_0^1(x^3+x)dx$ $=\bigg[\dfrac{1}{4}x^4+\dfrac{1}{2}x^2\bigg]_0^1$ $=(\dfrac{1}{4}+\dfrac{1}{2})-0$ $=\dfrac{3}{4}$.
- $\displaystyle\int_0^{\frac{\pi}{2}}\sin(u)du$ $=\bigg[-\cos(x)\bigg]_0^\frac{\pi}{2}$ $=-\cos(\frac{\pi}{2})+\cos(0)=1$.
- $\displaystyle\int_1^{e^2}\dfrac{1}{x}dx$ $=\bigg[\ln(x)\bigg]_1^{e^2}$ $=\ln(e^2)-\ln(1)=2$.
- $\displaystyle\int_0^1e^tdt$ $=\bigg[e^t\bigg]_0^1=e^1-e^0=e-1$
- Soit $f$ une fonction continue sur un intervalle $I$, et soit $a$ un réel de $I$.
Propriétés de l'intégrale.
- $\displaystyle\int_a^b(f(x)+g(x))dx=\displaystyle\int_a^bf(x)dx+\displaystyle\int_a^bg(x)dx$.
- $\displaystyle\int_a^b(\alpha\times f(x))dx=\alpha\times\displaystyle\int_a^bf(x)dx$.
- $I=\displaystyle\int_1^2e^xdx$ $=\bigg[e^x\bigg]_1^2=e(e-1)$
- $J=\displaystyle\int_1^2\dfrac{1}{2\sqrt{x}}dx=\bigg[\sqrt{x}\bigg]_1^2=\sqrt{2}-1$.
- Soit $f$ une fonction continue sur un intervalle $I$, $F$ est une primitive quelconque de $f$ sur $I$.
- Soit $g$ une fonction continue sur un intervalle $I$, $G$ est une primitive quelconque de $g$ sur $I$.
- La fonction $x\mapsto F(x)+G(x)$ est une primitive de la fonction $f+g$.
Donc $\displaystyle\int_a^b(f(x)+g(x))dx$ $=\bigg[F(x)+G(x)\bigg]_a^b$ $=(F(b)+G(b))-(F(a)+G(a))$ $=(F(b)-F(a))+(G(b)-G(a))$ $=\displaystyle\int_a^bf(x)dx+\displaystyle\int_a^bg(x)dx$. - La fonction $x\mapsto\alpha\times F(x)$ est une primitive de la fonction $\alpha\times f$.
Donc $\displaystyle\int_a^b(\alpha\times f(x))dx$ $=\bigg[\alpha\times F(x)\bigg]_a^b$ $=(\alpha\times F(b))-(\alpha\times F(a))$ $=\alpha\times (F(b)-F(a))$ $=\alpha\times\displaystyle\int_a^bf(x)dx$. - Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$, alors $\displaystyle\int_a^bf(t)dt\geq 0$.
- Soient $f$ et $g$ deux fonctions continues sur un intervalle $[a;b]$.
Si $a\leq b$ et pour tout $t\in[a;b]$ $f(t)\leq g(t)$, alors $\displaystyle\int_a^bf(t)dt\leq \displaystyle\int_a^bg(t)dt$. - Démontrer que pour tout $x\in[0;1]$, on a: $\dfrac{1}{2}\leq\dfrac{1}{1+x^2}\leq 1$.
- En déduire un encadrement de $\displaystyle\int_0^1\dfrac{1}{1+x^2}dx$.
- $x\in[0;1]$ $\Rightarrow$ $0\leq x^2\leq 1$ $\Rightarrow$ $1\leq 1+x^2\leq 2$.
Or la fonction $x\mapsto\dfrac{1}{x}$ est strictement décroissante sur $]0;+\infty[$, donc nous avons:
$1\leq 1+x^2\leq 2$ $\Rightarrow$ $\dfrac{1}{2}\leq\dfrac{1}{1+x^2}\leq\dfrac{1}{1}=1$. - Nous savons que pour tout $x\in[0;1]$, on a: $\dfrac{1}{2}\leq\dfrac{1}{1+x^2}\leq 1$.
Donc $\dfrac{1}{2}$, minore et $1$ majore la fonction $x\mapsto\dfrac{1}{1+x^2}$, donc on a:
$\dfrac{1}{2}\times(1-0)\leq\displaystyle\int_0^1\dfrac{1}{1+x^2}\leq 1\times(1-0)$ Intégration par parties.
- $u'(x)=x$, et donc $u(x)=\dfrac{1}{2}x^2$.
- $v(x)=ln(x)$ et donc $v'(x)=\dfrac{1}{x}$
Défintion.
Une fonction $f$ définie sur un intervalle $I=[a;b]$ $(a\leq b)$ est en escalier lorsqu'il existe $n+1$ nombres réels $x_i\in[a;b]$ tels que $x_0=a$, $x_n=b$ et $x_0;x_1;x_2;...;x_{n-1};x_n$ n+1 nombres strictement rangés par ordre croissant et tels que $f$ est constante sur chaque intervalle ouvert $]x_i;x_{i+1}[$, pour $0\leq i\leq n-1$.
Définition de l'intégrale d'une fonction en escalier.
Exemples d'intégrale de fonction en escalier.
Définition;
Soit $f$ une fonction continue et positive sur un intervalle $[a;b]$ et soit $\mathcal{C}_f$ la courbe représentative de $f$
dans un repère orthonormée $\mathcal{R}(O;\vec{i};\vec{j})$.
L'aire sous la courbe est l'aire du domaine limité par la $\mathcal{C}$, l'axe des abscisses et les droites verticales $x=a$ et $x=b$.
L'aire s'exprime en unité d'aire et l'unité d'aire est l'aire du rectangle $OIJK$ des unités.
L'intégrale de $f$ de $[a;b]$, notée $\displaystyle\int_a^bf(x)dx$ est l'aire sous la courbe sur l'intervalle $[a;b]$.
Interprétation graphique.

Méthode des rectangles (exemple).
Soit $f$ la fonction définie sur $[0;1]$ par $f(x)=\dfrac{1}{1+x^2}$.
$\mathcal{C}_f$ est la courbe représentative de $f$ dans repère orthogonal.
On découpe l'intervalle $[0;1]$ en $n$ intervalles réguliers à l'aide des nombres $x_0=0;x_1=\dfrac{1}{n};x_2=\dfrac{2}{n};...;x_{n-1}=\dfrac{n-1}{n};x_n=1$.
Comme la fonction $f$ est décroissante sur $[0;1]$, on pourrais démontrer que:
$\dfrac{1}{10}\bigg(f(0.1)+f(0.2)+...f(0.9)+f(1)\bigg) < \displaystyle\int_0^1 \dfrac{1}{1+x^2}dx$ $ < \dfrac{1}{10}\bigg(f(0)+f(0.1)+...f(0.8)+f(0.9)\bigg)$.
Utilisation d'un algorithme Python.



Propriétés algébriques.
Soient $f$ et $g$ deux fonctions continues sur l'intervalle $[a;b]$ et $\alpha\in\mathbb{R}$, on a:
Exemple.
-
$\displaystyle\int_0^1(\sqrt{3}e^x-\dfrac{3}{2\sqrt{x}})dx$ $=\sqrt{3}\times I-3\times J$ $=\sqrt{3}e(e-1)-3\sqrt{2}+3$.
Relation de Chasles.
Soit $f$ une fonction continue et positive sur $[a;b]$.
Pour tout $c\in[a;b]$, on a: $\displaystyle\int_a^bf(t)dt=\int_a^cf(t)dt+\int_c^bf(t)dt.$
Interprétation graphique.

Soit $f$ une fonction continue et positive sur $[a;b]$, nous savons d'après le théorème fondamental précédent qu'il existe une primitive $F$ de $f$
sur l'intervalle $[a;b]$.
On a $\displaystyle\int_a^cf(t)dt+\displaystyle\int_c^bf(t)dt=\bigg[F(t)\bigg]_a^c+\bigg[F(t)\bigg]_c^b$
$=\bigg(F(c)-F(a)\bigg)+\bigg (F(b)-F(c)\bigg )$ $=F(b)-F(a)=\displaystyle\int_a^b f(t)dt$.
Exemple.
Calculons l'intégrale $\displaystyle\int_{-2}^2|x^2-1|dx$.
Pour calculer nous devons exprimer $f(x)=|x^2-1|$ sans les barres de valeurs absolues. Nous avons:

Donc $\displaystyle\int_{-2}^2|x^2-1|dx$ $=\displaystyle\int_{-2}^{-1}x^2-1dx+\displaystyle\int_{-1}^{1}(1-x^2)dx+\displaystyle\int_{1}^{2}x^2-1dx$ $=\bigg[\dfrac{1}{3}x^3-x\bigg]_{-2}^{-1}+\bigg[x-\dfrac{1}{3}x^3\bigg]_{-1}^{1}+\bigg[\dfrac{1}{3}x^3-x\bigg]_{1}^{2}=4$.

Encadrement d'une intégrale (admis en terminale).
Interprétation graphique.
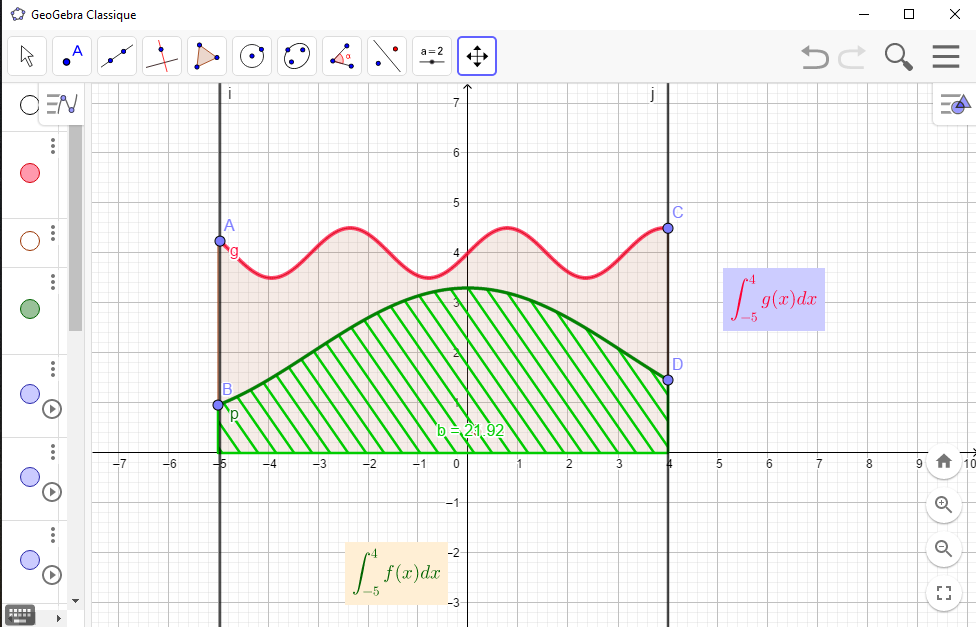
Soit $f$ une fonction continue sur un intervalle $I$, et soit $m$ et $M$ un minorant et un majorant de $f$ sur $[a;b]$.
Donc pour tout $x\in [a;b]$, on a $m\leq f(x)\leq M$ $\Rightarrow$ $\displaystyle\int_a^b mdx\leq\displaystyle\int_a^bf(x)dx\leq\displaystyle\int_a^b Mdx$, donc
$m(b-a)\leq\displaystyle\int_a^bf(x)dx\leq M(b-a)$
Théoréme.
Soit $f$ une fonction continue sur un intervalle $I$, et soit $m$ et $M$ un minorant et un majorant de $f$ sur $[a;b]$.
On a l'inégalité suivante: $m(b-a)\leq\displaystyle\int_a^bf(t)dt\leq M(b-a)$.
Interprétation graphique.

Exercice.
Propriété.
Soient $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ de $\mathbb{R}$, telles que u' et v' soient continues sur $I$.
Pour tout $a\in I$ et $b\in I$, $a < b$, alors:
$\displaystyle\int_a^b(u'(x)\times v(x)dx=\bigg[u(x)\times v(x)\bigg]_a^b-\displaystyle\int_a^b u(x)\times v'(x)dx$.
Comme les fonctions $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ de $\mathbb{R}$, on a:
$(u\times v)'(x)=u'(x)\times v(x)+u(x)\times v'(x)$, donc on a $\displaystyle\int_a^b (u\times v)'(x)dx=\displaystyle\int_a^b (u'(x)\times v(x)+u(x)\times v'(x))dx$, donc
$\displaystyle\int_a^b (u\times v)'(x)dx=\displaystyle\int_a^b u'(x)\times v(x)+\displaystyle\int_a^b u(x)\times v'(x)dx$.
Il est clair qu'une primitive possible de la fonction $g(x)=(u\times v)'(x)$ est la fonction $G(x)=u(x)\times v(x)$, donc nous avons l'égalité suivante:
$\displaystyle\int_a^b(u(x)\times v(x))'dx=\bigg[u(x)\times v(x)\bigg]_a^b$.
Donc $\bigg[u(x)\times v(x)\bigg]_a^b=\displaystyle\int_a^b u'(x)\times v(x)+\displaystyle\int_a^b u(x)\times v'(x)dx$.
Donc Pour tout $a\in I$ et $b\in I$, $a < b$, alors:
$\displaystyle\int_a^b(u'(x)\times v(x)dx=\bigg[u(x)\times v(x)\bigg]_a^b-\displaystyle\int_a^b u(x)\times v'(x)dx$.
Exemple.
Calculons l'intérale $\displaystyle\int_1^e x\times\ln(x)dx$.
Utilisons une intégration par partie, puisque il difficile d'obtenir rapidemant une primitive de la fonction $f$ définie par
$f(x)=x\ln(x)$ sur $]0;+\infty[$.
On ne connâit pas directememt la primitive de $ln(x)$, il vaut mieux rechercher une primitive de $x$, donc on pose:
$\Rightarrow$ $\displaystyle\int_1^e x\times\ln(x)dx$ $=\bigg[\dfrac{x^2}{2}\times\ln(x)\bigg]_1^e-\displaystyle\int_1^e \dfrac{x^2}{2}\times\dfrac{1}{x}dx$ $=\bigg(\dfrac{e^2}{2}\ln(e)-0\bigg)-\displaystyle\int_1^e \dfrac{x}{2}dx$ $=\dfrac{e^2}{2}-\bigg[\dfrac{x^2}{4}\bigg]_1^e$