Limites d'une fonction.
Limite infinie au voisinage de l'infini.
- Soit $f$ une fonction définie sur un intervalle de la forme $[A;+\infty[$ où $A$ est un réel, soit $\mathcal{C}$ la courbe représentative de $f$ et soit $l$ un réel.
Dire que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $+\infty$ signifie que $f(x)$ est aussi grand que l'on veut dès que $x$ est suffisamment grand.
On note cela par: $\displaystyle\lim_{x\to +\infty}f(x)=+\infty$. - Soit $f$ une fonction définie sur un intervalle de la forme $]-\infty;A]$ où $A$ est un réel, soit $\mathcal{C}$ la courbe représentative de $f$ et soit $l$ un réel.
Dire que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $-\infty$ signifie que $f(x)$ prend des valeurs aussi grande que l'on veut dès que $x$ prend des valeurs négatives de valeur absolue suffisamment grande.
On note cela par: $\displaystyle\lim_{x\to -\infty}f(x)=+\infty$. 
$\displaystyle\lim_{x\to +\infty}x=+\infty$- $\displaystyle\lim_{x\to +\infty}{x^2}=+\infty$
- $\displaystyle\lim_{x\to -\infty}{x^2}=+\infty$
- $\displaystyle\lim_{x\to +\infty}{\sqrt{x}}=+\infty$
- $\displaystyle\lim_{x\to +\infty}{(-\sqrt{x})}=-\infty$
- $\displaystyle\lim_{x\to -\infty}{x^3}=-\infty$
- $\displaystyle\lim_{x\to +\infty}(-x^5)=-\infty$
- Montrons que $\displaystyle\lim_{x\to +\infty}{x^2}=+\infty$.
Soit $A>0$ (aussi grand que l'on veut).
$x^2>A$ et $x\geq 0$ $\Leftrightarrow$ $x>\sqrt{A}$.
Si $x\in]\sqrt{A};+\infty[$ alors $x^2>A$. Donc nous avons $\displaystyle\lim_{x\to +\infty}{x^2}=+\infty$. - Montrons que $\displaystyle\lim_{x\to +\infty}{\sqrt{x}}=+\infty$.
Soit $A>0$ (aussi grand que l'on veut).
$\sqrt{x}>A$ $\Leftrightarrow$ $x>A^2$.
Si $x\in]A^2;+\infty[$ alors $\sqrt{x}>A$. Donc nous avons $\displaystyle\lim_{x\to +\infty}\sqrt{x}=+\infty$. - Il est clair que: $\displaystyle\lim_{x\to +\infty}{\sqrt{x}}=+\infty$ $\Leftrightarrow$ $\displaystyle\lim_{x\to +\infty}{-\sqrt{x}}=-\infty$.
- Montrons que $\displaystyle\lim_{x\to +\infty}{x^3}=+\infty$.
Soit $A>0$ (aussi grand que l'on veut).
$x^3>A$ $\Leftrightarrow$ $x>\sqrt[3]{A}$.
Si $x\in\bigg]\sqrt[3]{A};+\infty[$ alors $x^3>A$. Donc nous avons $\displaystyle\lim_{x\to +\infty}{x^3}=+\infty$. Limites finie a l'infini, asymptote horizontale.
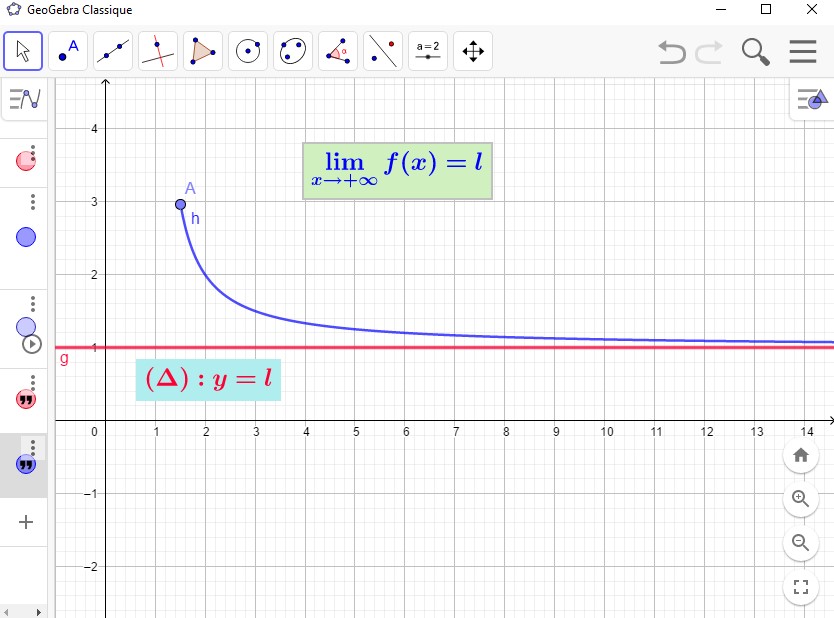
- Soit $f$ une fonction définie sur un intervalle de la forme $[A;+\infty[$ où $A$ est un réel, soit $\mathcal{C}$ la courbe représentative de $f$ et soit $l$ un réel.
Dire que $f(x)$ tend vers $l$ quand $x$ tend vers $+\infty$ signifie que $f(x)$ est aussi proche de la valeur $l$ que l'on veut dès que $x$ est suffisamment grand.
On note cela par: $\displaystyle\lim_{x\to +\infty}f(x)=l$. - Soit $f$ une fonction définie sur un intervalle de la forme $]-\infty;A]$ où $A$ est un réel, soit $\mathcal{C}$ la courbe représentative de $f$ et soit $l$ un réel.
Dire que $f(x)$ tend vers $l$ quand $x$ tend vers $-\infty$ signifie que $f(x)$ prend des valeurs aussi proche de $l$ que l'on veut dès que $x$ prend des valeurs négatives de valeur absolue suffisamment grande.
On note cela par: $\displaystyle\lim_{x\to -\infty}f(x)=l$. - Dans les deux cas précédents, on dit que la droite $\Delta:y=l$ est une asymptote horizontale à la courbe $\mathcal{C}_f$ en $+\infty$ et $-\infty$.
- $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{x}=0$
- $\displaystyle\displaystyle\lim_{x\to -\infty}\frac{1}{x}=0$
- $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{x^2}=0$
- $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{\sqrt{x}}=0$
- $\displaystyle\displaystyle\lim_{x\to +\infty}2+\frac{1}{x^3}=2$
- $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{x+1}{x}=1$
- Soit $\epsilon>0$ et $x>0$.
$0 <\dfrac{1}{x} < \epsilon$ et $x>0$ $\Leftrightarrow$ $x>\dfrac{1}{\epsilon}$.
Donc dés que $x>\dfrac{1}{\epsilon}$, alors $0 < \dfrac{1}{x} < \epsilon$, ce qui ce traduit par $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{x}=0$. - Soit $\epsilon>0$ et $x < 0$.
$-\epsilon <\dfrac{1}{x} < 0$ et $x < 0$ $\Leftrightarrow$ $x < -\dfrac{1}{\epsilon}$.
Donc dés que $x < -\dfrac{1}{\epsilon}$, alors $-\epsilon <\dfrac{1}{x} < 0$, ce qui ce traduit par $\displaystyle\displaystyle\lim_{x\to -\infty}\frac{1}{x}=0$. - Soit $\epsilon>0$ et $x>0$.
$0 <\dfrac{1}{x^2} < \epsilon$ et $x>0$ $\Leftrightarrow$ $x^2>\dfrac{1}{\epsilon}$ et $x>0$ $\Leftrightarrow$ $x>\sqrt{\dfrac{1}{\epsilon}}=\dfrac{1}{\sqrt{\epsilon}}$.
Donc dés que $x>\dfrac{1}{\sqrt{\epsilon}}$, alors $0 < \dfrac{1}{x^2} < \epsilon$, ce qui ce traduit par $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{x^2}=0$. - Soit $\epsilon>0$ et $x>0$.
$0 <\dfrac{1}{\sqrt{x}} < \epsilon$ et $x>0$ $\Leftrightarrow$ $\sqrt{x}>\dfrac{1}{\epsilon}$ $\Leftrightarrow$ $x>\dfrac{1}{\epsilon^2}$.
Donc dés que $x>\dfrac{1}{\epsilon^2}$, alors $0 < \dfrac{1}{\sqrt{x}} < \epsilon$, ce qui ce traduit par $\displaystyle\displaystyle\lim_{x\to +\infty}\frac{1}{\sqrt{x}}=0$. Limite finie en un réel.
- Lorsque $x_0\in\mathcal{D}_f$, on note $\displaystyle\lim_{x\to x_0}f(x)=l$.
- Lorsque $x_0$ est une borne réelle de $\mathcal{D}_f$.
- Si $\mathcal{D}_f=]x_0;+\infty[$ ou $\mathcal{D}_f=]x_0;b[$ ou bien $\mathcal{D}_f=]x_0;b]$ avec $x_0 < b$, on écrit alors $\displaystyle\lim_{x\to x_0,x_0\in\mathcal{D}_f}f(x)=\displaystyle\lim_{x\to x_0^+}f(x)=l$. On dit que $f$ a une limite finie à droite en $x_0$.
- Si $\mathcal{D}_f=]-\infty;x_0[$ ou $\mathcal{D}_f=]c;x_0[$ ou bien $\mathcal{D}_f=[c;x_0[$ avec $c < x_0$, on écrit alors $\displaystyle\lim_{x\to x_0,x_0\in\mathcal{D}_f}f(x)=\displaystyle\lim_{x\to x_0^-}f(x)=l$. On dit que $f$ a une limite finie à droite en $x_0$.
Limite infinie en un réel.
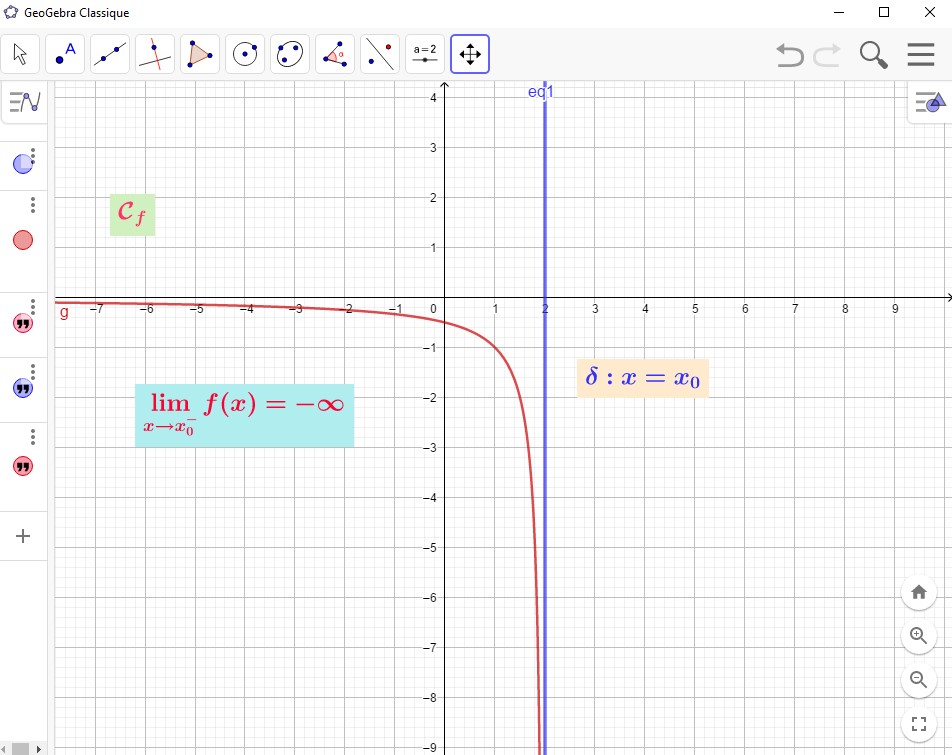
- Dire que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $x_0$ avec $x>x_0$ signifie que $f(x)$ est aussi grand que l'on veut dès que $x$ est suffisamment proche de $x_0$ avec $x>x_0$.
On note cela par: $\displaystyle\lim_{\begin{array}[pos]{c} x\to x_0\\ x>x_0\\ \end{array}}f(x)=\displaystyle\lim_{x\to x_0^+}f(x)=+\infty$. - Dire que $f(x)$ tend vers $-\infty$ quand $x$ tend vers $x_0$ avec $x>x_0$ signifie que $f(x)$ prend des valeurs négative de valeur absolue aussi grande que l'on veut dès que $x$ est suffisamment proche de $x_0$ avec $x>x_0$.
On note cela par: $\displaystyle\lim_{\begin{array}[pos]{c} x\to x_0\\ x>x_0\\ \end{array}}f(x)=\displaystyle\lim_{x\to x_0^+}f(x)=-\infty$. - Dans les deux cas précédents, on dit que la droite $\Delta:x=x_0$ est une asymptote verticale à la courbe $\mathcal{C}_f$ à droite de $x_0$.
- Dire que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $x_0$ avec $x < x_0$ signifie que $f(x)$ est aussi grand que l'on veut dès que $x$ est suffisamment proche de $x_0$ avec $x < x_0$.
On note cela par:$\displaystyle\lim_{\begin{array}[pos]{c} x\to x_0\\ x < x_0\\ \end{array}}f(x)=\lim_{x\to x_0^-}f(x)=+\infty$. - Dire que $f(x)$ tend vers $-\infty$ quand $x$ tend vers $x_0$ avec $x < x_0$ signifie que $f(x)$ prend des valeurs négatives de valeur absolue aussi grande
que l'on veut dès que $x$ est suffisamment proche de $x_0$ avec $x < x_0$.
On note cela par: $\displaystyle\lim_{\begin{array}[pos]{c} x\to x_0\\ x < x_0\\ \end{array}}f(x)=\lim_{x\to x_0^-}f(x)=-\infty$. - Dans les deux cas précédents, on dit que la droite $\Delta:x=x_0$ est une asymptote verticale à la courbe $\mathcal{C}_f$ à gauche de $x_0$.
- $\displaystyle\displaystyle\lim_{x\to 0^+}\frac{1}{x}=+\infty$
- $\displaystyle\displaystyle\lim_{x\to 0^-}\frac{1}{x^2}=-\infty$
- $\displaystyle\displaystyle\lim_{x\to 0^+}\frac{1}{\sqrt{x}}=+\infty$
- $\displaystyle\displaystyle\lim_{x\to 0^+}\frac{1}{x^2}=+\infty$
- $\displaystyle\displaystyle\lim_{x\to 0^-}\frac{1}{x^2}=+\infty$
- $\displaystyle\displaystyle\lim_{x\to 0^-}\frac{1}{x^3}=-\infty$
- $\displaystyle\displaystyle\lim_{x\to 1^-}\frac{1}{x-1}=-\infty$
- $\displaystyle\displaystyle\lim_{x\to 1^+}\frac{1}{x-1}=+\infty$
- $\displaystyle\displaystyle\lim_{x\to +\infty}f(x)=2$.
- $\displaystyle\displaystyle\lim_{x\to -\infty}f(x)=2$.
- $\displaystyle\displaystyle\lim_{x\to -2^-}f(x)=+\infty$.
- $\displaystyle\displaystyle\lim_{x\to -2^+}f(x)=-\infty$.
- $\displaystyle\displaystyle\lim_{x\to 1^-}f(x)=-\infty$.
- $\displaystyle\displaystyle\lim_{x\to 1^+}f(x)=+\infty$.
- Les droites d'équations $x=-2$ et $x=1$ sont des asymptotes verticales à $\mathcal{C}_f$.
- La droite d'équation $y=2$ est asymptote horizontale à $\mathcal{C}_f$ au voisinage de $-\infty$ et $+\infty$.
Opérations sur les limites.
- Soient $f(x)=\dfrac{1}{x^2}+2$ et $g(x)=-1+\dfrac{2}{x}$ pour tout $x\not=0$.
$\displaystyle\lim_{x\to +\infty}(f(x)+g(x))=\displaystyle\lim_{x\to +\infty}f(x)+\displaystyle\lim_{x\to +\infty}g(x)$
Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x^2}=0$ et $\displaystyle\lim_{x\to +\infty}\dfrac{2}{x}=0$; on en déduit que $\displaystyle\lim_{x\to +\infty}f(x)=2$ et $\displaystyle\lim_{x\to +\infty}g(x)=-1$. Donc on a: $\displaystyle\lim_{x\to +\infty}(f(x)+g(x))=2+(-1)=1$. - Soit $f(x)=x^2$ et $g(x)=2x$ pour tout $x\not=0$.
$\displaystyle\lim_{x\to 1}(f(x)+g(x))=\displaystyle\lim_{x\to 1}f(x)+\displaystyle\lim_{x\to 1}g(x)$
Nous savons que $\displaystyle\lim_{x\to 1}\dfrac{1}{x^2}=1$ et $\displaystyle\lim_{x\to 1}\dfrac{2}{x}=2$. Donc on a: $\displaystyle\lim_{x\to +\infty}(f(x)+g(x))=\displaystyle\lim_{x\to +\infty}(x^2+2x)=1+2=3$. - Soit $f(x)=x^2+[\dfrac{1}{x}+1]$ pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to +\infty} x^2=+\infty$ et $\displaystyle\lim_{x\to +\infty}[\dfrac{1}{x}+1]=1$, donc nous avons $\displaystyle\lim_{x\to +\infty} x^2+[\dfrac{1}{x}+1]=+\infty$. - Soit $f(x)=(x^2+1)+\dfrac{1}{x}$ pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to 0^+} x^2+1=0+1=1$ et $\displaystyle\lim_{x\to 0^+}\dfrac{1}{x}=+\infty$, donc nous avons $\displaystyle\lim_{x\to +\infty} (x^2+1)+\dfrac{1}{x}=+\infty$. - Soit $f(x)=-2x^2+[\dfrac{2}{x}+5]$ pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to +\infty} -2x^2=-\infty$ et $\displaystyle\lim_{x\to +\infty}[\dfrac{2}{x}+5]=5$, donc nous avons $\displaystyle\lim_{x\to +\infty} -2x^2+[\dfrac{2}{x}+5]=-\infty$. - Soit $f(x)=(-2x^2+6)+[\dfrac{1}{x}]$ pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to 0^-} -2x^2+6=6$ et $\displaystyle\lim_{x\to 0^-}\dfrac{1}{x}=-\infty$, donc nous avons $\displaystyle\lim_{x\to +\infty} (-2x^2+6)+\dfrac{1}{x}=-\infty$. - Soit $f(x)=2x^2+5x$ pour tout $x\in\mathbb{R}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} 2x^2=+\infty$ et $\displaystyle\lim_{x\to +\infty} 5x=+\infty$, donc nous avons $\displaystyle\lim_{x\to +\infty} 2n^2+5n=+\infty$. - Soit $g(x)=\dfrac{1}{x}+\dfrac{1}{x^3}$, pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to 0^+}\dfrac{1}{x}=+\infty$ et $\displaystyle\lim_{x\to 0^+}\dfrac{1}{x^3}=+\infty$, donc nous avons $\displaystyle\lim_{x\to 0^+}\bigg(\dfrac{1}{x}+\dfrac{1}{x^3}\bigg)=+\infty$. - Soit $f(x)=-x^2-3x=(-x^2)+(-3x)$ pour tout $x\in\mathbb{R}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} -x^2=-\infty$ et $\displaystyle\lim_{x\to +\infty} (-3x)=-\infty$, donc nous avons $\displaystyle\lim_{x\to +\infty}f(x)$ $=\displaystyle\lim_{x\to +\infty} -x^2-3x=-\infty$. - Soit $g(x)=\dfrac{-1}{x}+\dfrac{1}{x^3}$, pour tout $x\not=0$.
Nous savons que $\displaystyle\lim_{x\to 0^-}\dfrac{1}{x}=-\infty$ et $\displaystyle\lim_{x\to 0^-}\dfrac{1}{x^3}=-\infty$, donc nous avons $\displaystyle\lim_{x\to 0^-}\bigg(\dfrac{1}{x}+\dfrac{1}{x^3}\bigg)=-\infty$. - Soient deux fonctions $f(x)=n^2$ et $g(x)=3n$ définies sur $\mathbb{R}$. Calculons $\displaystyle\lim_{x\to +\infty} f(x)-g(x)=\displaystyle\lim_{x\to +\infty} x^2-3x$.
Nous sommes en présence d'une forme indéterminée de la forme $\infty-\infty$.
- Méthode 1: factorisons par le plus haut degré ici $x^2$. On a $x^2-3x=x^2(1-\dfrac{3}{x})$, pour tout $x\not=0$.
Or $\displaystyle\lim_{x\to +\infty}x^2=+\infty$ et $\displaystyle\lim_{x\to +\infty}(1-\dfrac{3}{x})=1$, donc d'aprés le tableau sur les limites d'un produit de suites, on a: $\displaystyle\lim_{x\to +\infty}x^2(1-\dfrac{3}{x})=+\infty$. - Méthode 2: On pourrait ici simplifier simplement par $x$. On a $x^2-3x=x(x-3)$ pour tout $n\in\mathbb{R}$.
Or $\displaystyle\lim_{x\to +\infty}x=+\infty$ et $\displaystyle\lim_{x\to +\infty}(x-3)=+\infty$, donc d'aprés le tableau sur les limites d'un produit de suites, on a: $\displaystyle\lim_{x\to +\infty}x(x-3)=+\infty$.
- Méthode 1: factorisons par le plus haut degré ici $x^2$. On a $x^2-3x=x^2(1-\dfrac{3}{x})$, pour tout $x\not=0$.
- Soient deux fonctions $f(x)=x^2$ et $g(x)=x^3$ définies sur $\mathbb{R}$. Calculons $\displaystyle\lim_{x\to +\infty} f(x)-g(x)=\displaystyle\lim_{x\to +\infty} x^2-x^3$.
Nous sommes en présence d'une forme indéterminée de la forme $\infty-\infty$.
- Méthode 1: factorisons par le plus haut degré ici $x^3$. On a $x^2-x^3=x^3(\dfrac{1}{x}-1)$, pour tout $x\not=0$.
Or $\displaystyle\lim_{x\to +\infty}x^3=+\infty$ et $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x}-1)=-1$, donc d'aprés le tableau sur les limites d'un produit de suites, on a: $\displaystyle\lim_{x\to +\infty}x^3(\dfrac{1}{x}-1)=-\infty$. - Méthode 2: On pourrait ici simplifier simplement par $x^2$. On a $x^2-x^3=x^2(1-x)$ pour tout $n\in\mathbb{R}$.
Or $\displaystyle\lim_{x\to +\infty}x^2=+\infty$ et $\displaystyle\lim_{x\to +\infty}(1-x)=-\infty$, donc d'aprés le tableau sur les limites d'un produit de suites, on a: $\displaystyle\lim_{x\to +\infty}x^2(1-x)=-\infty$.
- Méthode 1: factorisons par le plus haut degré ici $x^3$. On a $x^2-x^3=x^3(\dfrac{1}{x}-1)$, pour tout $x\not=0$.
- Soit $f(x)=\dfrac{1}{x^2}$ pour tout $x\geq 1$, et soit $g(x)=x^3+3x+5$ pour tout $x\geq 1$.
Calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x^2})(x^3+3x+5)$.
Nous avons $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x^2})=0$ et $\displaystyle\lim_{x\to +\infty}(x^3+3x+5)=+\infty$. Nous sommes en présence d'une forme indéterminée de la forme $0\times\infty$.
Développons $f(x)\times g(x)=\dfrac{1}{x^2}\times x^3+3x\times\dfrac{1}{x^2}+\dfrac{5}{x^2}$ $=x+\dfrac{3}{x}+\dfrac{5}{x^2}$. Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{3}{x}+\dfrac{5}{x^2}=0+0=0$ et $\displaystyle\lim_{x\to +\infty}x=+\infty$, donc par addition des limites on obtient que:
$\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}x+\dfrac{3}{x}+\dfrac{5}{x^2}=+\infty$. - Soit $f(x)=\dfrac{1}{x^3}$ pour tout $x\geq 1$, et soit $g(x)=x^3+3x^2$ pour tout $x\geq 1$.
Calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x^3})(x^3+3x^2)$.
Nous avons $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x^3})=0$ et $\displaystyle\lim_{x\to +\infty}(x^3+3x^2)=+\infty$. Nous sommes en présence d'une forme indéterminée de la forme $0\times\infty$.
Développons $f(x)\times g(x)=\dfrac{1}{x^3}\times x^3+3x^2\times\dfrac{1}{x^3}$ $=1+\dfrac{3}{x}$. Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{3}{x}=0$ , donc $\displaystyle\lim_{x\to +\infty}(1+\dfrac{3}{x})=1$.
$\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=1$. - Soit $f(x)=\dfrac{3}{x^2}$ pour tout $x\geq 1$, et soit $g(x)=x-2$ pour tout $x\geq 1$.
Calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}(\dfrac{3}{x^2})(x-2)$.
Nous avons $\displaystyle\lim_{x\to +\infty}(\dfrac{3}{x^2})=0$ et $\displaystyle\lim_{x\to +\infty}(x-2)=+\infty$. Nous sommes en présence d'une forme indéterminée de la forme $0\times\infty$.
Développons $f(x)\times g(x)=\dfrac{3}{x^2}\times (x-2)$ $=\dfrac{3}{x}-\dfrac{6}{x^2}$. Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{3}{x}=0$, et $\displaystyle\lim_{x\to +\infty}\dfrac{6}{x^2}=0$.
Donc $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=0-0=0$. Cas ou $\displaystyle\lim_{x\to a}g(x)\not=0$.
$\displaystyle\lim_{x\to a}f(x)$ $l$ $l$ $+\infty$ $+\infty$ $-\infty$ $-\infty$ $+\infty$ ou $-\infty$ $\displaystyle\lim_{x\to a}g(x)$ $l'\not=0$ $+\infty$ ou $-\infty$ $l'>0$ $l' < 0$ $l'>0$ $l' < 0$ $+\infty$ ou $-\infty$ $\displaystyle\lim_{x\to a}\bigg(\dfrac{f(x)}{g(x)}\bigg)$ $\dfrac{l}{l'}$ 0 $+\infty$ $-\infty$ $-\infty$ $+\infty$ forme indéterminée Cas ou $\displaystyle\lim_{x\to a}g(x)=0$.
$\displaystyle\lim_{x\to a}f(x)$ $l>0$ ou $+\infty$ $l>0$ ou $+\infty$ $l < 0$ ou $-\infty$ $l < 0$ ou $-\infty$ 0 $\displaystyle\lim_{x\to a}g(x)$ 0 en restant positive 0 en restant négative 0 en restant positive 0 en restant négative 0 $\displaystyle\lim_{x\to a}\bigg(\dfrac{f(x)}{g(x)}\bigg)$ $+\infty$ $-\infty$ $-\infty$ $+\infty$ forme indéterminée - Soit $f(x)=2x^2+x$ et $g(x)=5x+3$ pour tout $n\in\mathbb{R}$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(2x^2+x)}{(5x+3)}$. Nous savons que $\displaystyle\lim_{x\to +\infty}(2x^2+x)=+\infty$ et $\displaystyle\lim_{x\to +\infty}(5x+3)=+\infty$.
Nous sommes en présence d'une forme indéterminée de la forme $\dfrac{\infty}{\infty}$.
Pour tout $x\not=0$, on a: $\dfrac{f(x)}{g(x)}=\dfrac{(2x^2+x)}{(5x+3)}$ $=\dfrac{x(2x+1)}{x(5+\dfrac{3}{x})}$ $=\dfrac{(2x+1)}{(5+\dfrac{3}{x})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(2x+1)=+\infty$ et $\displaystyle\lim_{x\to +\infty}(5+\dfrac{3}{x})=5$.
On en déduit grâce aux propriétés opératoires du quotient des limites que:$\displaystyle\lim_{x\to +\infty}\dfrac{(2x^2+x)}{(5x+3)}$ $=\displaystyle\lim_{x\to +\infty}\dfrac{(2x+1)}{(5+\dfrac{3}{x})}=+\infty$. - Soit $f(x)=n^2+n$ et $g(x)=5n^2+3$ pour tout $n\in\mathbb{R}$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(x^2+x)}{(5x^2+3)}$. Nous savons que $\displaystyle\lim_{x\to +\infty}(x^2+x)=+\infty$ et $\displaystyle\lim_{x\to +\infty}(5x^2+3)=+\infty$.
Nous sommes en présence d'une forme indéterminée de la forme $\dfrac{\infty}{\infty}$.
Pour tout $x\not=0$, on a: $\dfrac{f(x)}{g(x)}=\dfrac{(x^2+x)}{(5x^2+3)}$ $=\dfrac{x^2(1+\dfrac{1}{x})}{x^2(5+\dfrac{3}{x^2})}$ $=\dfrac{(1+\dfrac{1}{x})}{(5+\dfrac{3}{x^2})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(1+\dfrac{1}{x})=1$ et $\displaystyle\lim_{x\to +\infty}(5+\dfrac{3}{x^2})=5$.
On en déduit grâce aux propriétés opératoires du quotient des limites que:$\displaystyle\lim_{x\to +\infty}\dfrac{(x^2+x)}{(5x^2+3)}$ $=\displaystyle\lim_{x\to +\infty}\dfrac{(1+\dfrac{1}{x})}{(5+\dfrac{3}{x^2})}=\dfrac{1}{5}$. - Soit $f(x)=n^2$ et $g(x)=n^3+3n$ pour tout $n\in\mathbb{R}$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{x^2}{(x^3+3x)}$. Nous savons que $\displaystyle\lim_{x\to +\infty} x^2=+\infty$ et $\displaystyle\lim_{x\to +\infty}(x^3+3x)=+\infty$.
Nous sommes en présence d'une forme indéterminée de la forme $\dfrac{\infty}{\infty}$.
Pour tout $n\not=0$, on a: $\dfrac{f(x)}{g(x)}=\dfrac{x^2}{(x^3+3x)}$ $=\dfrac{x^2}{x^2(x+\dfrac{3}{x})}$ $=\dfrac{1}{(x+\dfrac{3}{x})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(x+\dfrac{3}{x})=+\infty$.
On en déduit grâce aux propriétés opératoires du quotient des limites que:$\displaystyle\lim_{x\to +\infty}\dfrac{x^2}{(x^3+3x)}$ $=\displaystyle\lim_{x\to +\infty}\dfrac{1}{(x+\dfrac{3}{x})}=0$. - Soit $f(x)=x+2$ et $g(x)=\dfrac{5}{x}+\dfrac{3}{x^2}$ pour tout $x\not=0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(x+2)}{\dfrac{5}{x}+\dfrac{3}{x^2}}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} x+2=+\infty$ et $\displaystyle\lim_{x\to +\infty}\dfrac{5}{x}+\dfrac{3}{x^2}=0$. De plus pour tout $x>0$, il est clair que $\dfrac{5}{n}+\dfrac{3}{n^2}>0$, donc la fonction $g$ converge vers 0 tout en restant positive, on note cela: $\displaystyle\lim_{x\to +\infty}\dfrac{5}{x}+\dfrac{3}{x^2}=0^+$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(x+2)}{\dfrac{5}{x}+\dfrac{3}{x^2}}=+\infty$. - Soit $f(x)=2+\dfrac{1}{x}$ et $g(x)=\dfrac{1}{x}+\dfrac{1}{x^2}$ pour tout $x>0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(2+\dfrac{1}{x})}{\dfrac{1}{x}+\dfrac{1}{x^2}}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} 2+\dfrac{1}{x}=2$ et $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x}+\dfrac{1}{x^2}=0$. De plus pour tout $x>0$, il est clair que $\dfrac{1}{x}+\dfrac{1}{x^2}>0$, donc la fonction $g$ converge vers 0 tout en restant positive, on note cela: $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x}+\dfrac{1}{x^2}=0^+$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(2+\dfrac{1}{x})}{\dfrac{1}{x}+\dfrac{1}{x^2}}=+\infty$. - Soit $f(x)=\dfrac{1}{x}$ et $g(x)=\dfrac{1}{x}+\dfrac{1}{x^2}$ pour tout $x>0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{\dfrac{1}{x}}{\dfrac{1}{x}+\dfrac{1}{x^2}}$. Nous savons que $\displaystyle\lim_{x\to +\infty} (\dfrac{1}{x})=0$ et $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x}+\dfrac{1}{x^2})=0$.
Nous sommes en présence d'une forme indéterminée de la forme $\dfrac{0}{0}$.
Pour tout $x>0$ simplifions le quotient par $\dfrac{1}{x}$, on a: $\dfrac{f(x)}{g(x)}=\dfrac{\dfrac{1}{x}}{(\dfrac{1}{x}+\dfrac{1}{x^2})}$ $=\dfrac{\dfrac{1}{x}}{\dfrac{1}{x}\times(1+\dfrac{1}{x})}$ $=\dfrac{1}{(1+\dfrac{1}{x})}$ pour tout $x>0$.
Nous savons que: $\displaystyle\lim_{x\to +\infty}(1+\dfrac{1}{x})=1$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{\dfrac{1}{x}}{(\dfrac{1}{x}+\dfrac{1}{x^2})}$ $=\displaystyle\lim_{x\to +\infty}\dfrac{1}{(1+\dfrac{1}{x})}=\dfrac{1}{1}=1$. - Soit $f(x)=\dfrac{2}{x^3}$ et $g(x)=\dfrac{3}{x}+\dfrac{1}{x^2}$ pour tout $x>0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{\dfrac{2}{x^3}}{\dfrac{3}{x}+\dfrac{1}{x^2}}$. Nous savons que $\displaystyle\lim_{x\to +\infty} (\dfrac{2}{x^3})=0$ et $\displaystyle\lim_{x\to +\infty}(\dfrac{3}{x}+\dfrac{1}{x^2})=0$.
Nous sommes en présence d'une forme indéterminée de la forme $\dfrac{0}{0}$.
Pour tout $x>0$ simplifions le quotient par $\dfrac{1}{x}$, on a: $\dfrac{f(x)}{g(x)}=\dfrac{\dfrac{2}{x^3}}{(\dfrac{3}{x}+\dfrac{1}{x^2})}$ $=\dfrac{\dfrac{1}{x}\times\dfrac{2}{x^2}}{\dfrac{1}{x}\times(3+\dfrac{1}{x})}$ $=\dfrac{\dfrac{2}{x^2}}{(3+\dfrac{1}{x})}$ pour tout $x>0$.
Nous savons que: $\displaystyle\lim_{x\to +\infty}(3+\dfrac{1}{x})=3$ et $\displaystyle\lim_{x\to +\infty}\dfrac{2}{x^2}=0$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{\dfrac{2}{x^3}}{(\dfrac{3}{x}+\dfrac{1}{x^2})}$ $=\displaystyle\lim_{x\to +\infty}\dfrac{\dfrac{2}{x^2}}{(3+\dfrac{1}{x})}=\dfrac{0}{3}=0$. - Soit $f$ la fonction définie sur $\mathbb{R}-\{1\}$ par $f(x)=\dfrac{1}{x^2-1}$.
- Soit $g$ la fonction définie sur $\mathbb{R}-\{2;3\}$ par $g(x)=\dfrac{-1}{x^2-5x+6}$.
Théorèmes de comparaison sur les limites.
- Pour tout $x\in I=[b;+\infty[$, on a $g(x)\leq f(x)\leq h(x)$
- $\displaystyle\lim_{x\to +\infty}g(x)=l$ $\Rightarrow$ Il existe un réel $A>0$ tel que, pour tout $x\in]A;+\infty[$; alors $l-\epsilon < g(x) < l+\epsilon$.
- $\displaystyle\lim_{x\to +\infty}h(x)=l$ $\Rightarrow$ Il existe un réel $A'>0$ tel que, pour tout $x\in]A;+\infty[$; alors $l-\epsilon < h(x) < l+\epsilon$.
- Si pour tout $x\in I$ on a $g(x)\leq f(x)$ et si $\displaystyle\lim_{x\to +\infty}g(x)=+\infty$ alors $\displaystyle\lim_{x\to +\infty}f(x)=+\infty$.
- Si pour tout $x\in I$ on a $f(x)\leq g(x)$ et si $\displaystyle\lim_{x\to +\infty}g(x)=-\infty$ alors $\displaystyle\lim_{x\to +\infty}f(x)=-\infty$.
- Soit la fonction $f$ définie pour tout $x\in]0;+\infty[$, par $f(x)=\dfrac{x^2-\cos(x)}{x}$.
Calculer la limite de la fonction $f$ au voisinage de $+\infty$. - Soit la fonction $g$ définie pour tout $x\in\mathbb{R}$, par $g(x)=2sin(x)-x^2$.
Calculer la limite de la fonction $g$ en $-\infty$. - Nous savons que pour tout $x\in I=[b;+\infty[$ on a $g(x)\leq f(x)$.
Soit $A>0$ (aussi grand que l'on veut), puisque $\displaystyle\lim_{x\to +\infty}v_n=+\infty$, il existe un entier $\eta$ tel que, pour tout $x\in]\eta;+\infty[$, alors $g(x)> A$.
Posons $N=max(p;\eta)$, dés que $x>\eta$ les deux propriétés précédentes sont vérifiées. Donc pour tout $x>\eta$, on a $f(x)\geq g(x)$ et $g(x)>A$, donc $f(x)\geq g(x)> A$.
Donc pour tout $x>\eta$, $f(x)> A$, donc $\displaystyle\lim_{x\to +\infty}f(x)=+\infty$. - Nous savons que pour tout $x\in I=[b;+\infty[$ on a $f(x)\leq g(x)$.
Soit $A < 0$ (aussi petit que l'on veut), puisque $\displaystyle\lim_{x\to +\infty}g(x)=-\infty$, il existe un entier $\eta$ tel que, pour tout $x\in]\eta;+\infty[$, alors $g(x) < A$.
Posons $N=max(p;\eta)$, dés que $x>\eta$ les deux propriétés précédentes sont vérifiées. Donc pour tout $x>\eta$, on a $f(x)\leq g(x)$ et $g(x) < A$, donc $f(x)\leq g(x) < A$.
Donc pour tout $x>\eta$, $f(x) < A$, donc $\displaystyle\lim_{x\to +\infty}f(x)=-\infty$. La fonction $x\mapsto\cos(x)$, n'admet pas de limite en $+\infty$, on ne peut donc pas utiliser les régles algébrique sur les limites.
Pour résoudre ce problème nous allons encadrer la fonction $f$, afin de pouvoir utiliser le théorème de comparaison des limites.
Pour tout $x\in]0;+\infty$, on a: $-1\leq\cos(x)\leq 1$ $\Leftrightarrow$ $x^2-1\leq\ x^2-\cos(x)\leq x^2+1$.
Puisque $x>0$, on a $\dfrac{x^2-1}{x}\leq\dfrac{x^2-\cos(x)}{x}\leq\dfrac{x^2+1}{x}$ $\Leftrightarrow$ $x-\dfrac{1}{x}\leq\dfrac{x^2-\cos(x)}{x}\leq\ x+\dfrac{1}{x}$.
Nous savons clairement que: $\displaystyle\lim_{x\to +\infty}\bigg(x-\dfrac{1}{x}\bigg)=+\infty$.
La seule inégalité qui est importante pour nous est: $\bigg(x-\dfrac{1}{x}\bigg)\leq\dfrac{x^2-\cos(x)}{x}$.
Donc d'après le théorème de comparaison des limites, on peut conclure que $\displaystyle\lim_{x\to +\infty}\dfrac{x^2-\cos(x)}{x}=+\infty$.La fonctio $x\mapsto\sin(x)$, n'admet pas de limite, on ne peut donc pas utiliser les régles algébrique sur les limites.
Pour résoudre ce problème nous allons encadrer la fonction $g$, afin de pouvoir utiliser le théorème de comparaison des limites.
Pour tout $x\in\mathbb{R}$, on a: $-1\leq\sin(x) \leq 1$ $\Leftrightarrow$ $-2\leq\ 2\sin(x)\leq 2$ $\Leftrightarrow$ $-2-x^2\leq 2\sin(x)-x^2 \leq\ 2-x^2$.
Nous savons clairement que: $\displaystyle\lim_{x\to -\infty}2-x^2=-\infty$.
La seule inégalité qui est importante pour nous est: $2\sin(x)-x^2 \leq\ 2-x^2$.
Donc d'après le théorème de comparaison des limites, on peut conclure que $\displaystyle\lim_{x\to -\infty}2\sin(x)-x^2=-\infty$.
Définition.
Interprétation graphique.
Exemples.
Définition.
Interprétation graphique.
Exemples.
Définition.
Dire qu'une fonction $f$ a pour limite le nombre réel $l$ en $x_0$ signifie que $f(x)$ est aussi proche de $l$ que l'on veut dès que $x$ est "assez proches" de $x_0$ en restant dans le domaine de définition de $f$.
Remarque.
Lorsqu'une fonction $f$ a pour limite $l$ en $x_0$, on note cela par $\displaystyle\lim_{x\to x_0,x_0\in\mathcal{D}_f}f(x)=l.$ Trois cas se présentent.Soit $x_0$ un réel et $f$ une fonction définie au voisinage de $x_0$ à droite et/ou à gauche, mais non définie en $x_0$.
C'est à dire que nous sommes dans les cas suivants $]-\infty;x_0[\cap\mathcal{D}_f\not=\emptyset$, ou $]x_0;+\infty[\cap\mathcal{D}_f\not=\emptyset$,
ou $]x_0-\epsilon;x_0+\epsilon[\cap\mathcal{D}_f\not=\emptyset$.
Limite infinie à droite.
Interprétation graphique.
Limite infinie à gauche.
Interprétation graphique.
Exemples.
Exemple de lecture graphique des limites d'une fonction.
Dans cette section la lettre $a$ désigne soit un nombre réel, soit $+\infty$, soit $-\infty$.
Limite d'une somme de fonctions.
| $\displaystyle\lim_{x\to a}f(x)$ | $l$ | $l$ | $l$ | $+\infty$ | $-\infty$ | $+\infty$ |
| $\displaystyle\lim_{x\to a}g(x)$ | $l'$ | $+\infty$ | $-\infty$ | $+\infty$ | $-\infty$ | $-\infty$ |
| $\displaystyle\lim_{x\to a}f(x)+g(x)$ | $l+l'$ | $+\infty$ | $-\infty$ | $+\infty$ | $-\infty$ | forme indéterminée. |
Voici quelques exemples de résolutions d'indéterminées du type $\infty-\infty$.
Limite d'un produit de fonctions.
| $\displaystyle\lim_{x\to a}f(x)$ | l | $l < 0$ ou $-\infty$ | $l>0$ ou $+\infty$ | $l < 0$ ou $-\infty$ | $l>0$ ou $+\infty$ | 0 |
| $\displaystyle\lim_{x\to a}g(x)$ | l' | $+\infty$ | $+\infty$ | $-\infty$ | $-\infty$ | $-\infty$ ou $+\infty$ |
| $\displaystyle\lim_{x\to a}f(x)\times g(x)$ | $l \times l'$ | $-\infty$ | $+\infty$ | $+\infty$ | $-\infty$ | forme indéterminée. |
Calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}\bigg(\dfrac{1}{x^2}+2\bigg)\bigg(-1+\dfrac{2}{x}\bigg)$.
Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x^2}=0$ et $\displaystyle\lim_{x\to +\infty}\dfrac{2}{x}=0$; on en déduit que $\displaystyle\lim_{x\to +\infty}\bigg(\dfrac{1}{x^2}+2\bigg)=2$
et $\displaystyle\lim_{x\to +\infty}\bigg(-1+\dfrac{2}{x}\bigg)=-1$.
On en déduit grâce aux propriétés opératoires du produit des limites que: $\displaystyle\lim_{x\to +\infty}\bigg(\dfrac{1}{x^2}+2\bigg)\bigg(-1+\dfrac{2}{x}\bigg)=2\times(-1)=-2$.
Soit $f(x)=-2+\dfrac{1}{x^3}$ et $g(x)=x+3$ deux fonction définies pour $x\not=0$,
calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}(-2+\dfrac{1}{x^3})(x+3)$.
Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x^3}=0$, donc $\displaystyle\lim_{x\to +\infty}(-2+\dfrac{1}{x^3})=-2$ et on a
$\displaystyle\lim_{x\to +\infty}(x+3)=+\infty$.
On en déduit grâce aux propriétés opératoires du produit des limites que: $\displaystyle\lim_{x\to +\infty}(-2+\dfrac{1}{x^3})(x+3)=-\infty$.
Soit $f(x)=3-\dfrac{2}{x}+\dfrac{1}{x^3}$ et $g(x)=5x^2-6$ deux fonctions définies sur $\mathbb{R}^\star$,
calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to +\infty}(3-\dfrac{2}{x}+\dfrac{1}{n^3})(5x^2-6)$.
Nous savons que $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x}=0$, $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x^3}=0$, donc $\displaystyle\lim_{x\to +\infty}(3-\dfrac{2}{x}+\dfrac{1}{x^3})=3$ et on a
$\displaystyle\lim_{x\to +\infty}(5x^2-6)=+\infty$.
On en déduit grâce aux propriétés opératoires du produit des limites que: $\displaystyle\lim_{x\to +\infty}(3-\dfrac{2}{x}+\dfrac{1}{x^3})(5x^2-6)=+\infty$.
Soit $f(x)=-2+x$ et $g(x)=-\dfrac{1}{x}+5$ deux fonctions définies sur $\mathbb{R}^\star$,
calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to 0^+}(-2+x)(-\dfrac{1}{x}+5)$.
Nous savons que $\displaystyle\lim_{x\to 0^+}(-2+x)=-2$ et on a
$\displaystyle\lim_{x\to 0^+}(-\dfrac{1}{x}+5)=-\infty$.
On en déduit grâce aux propriétés opératoires du produit des limites que: $\displaystyle\lim_{x\to 0^+}(-2+x)(-\dfrac{1}{x}+5)=+\infty$.
Soit $f(x)=3+2x$ et $g(x)=\dfrac{1}{x^3}+5$ deux suites définies sur $\mathbb{R}^\star$,
calculons $\displaystyle\lim_{x\to +\infty} f(x)\times g(x)=\displaystyle\lim_{x\to 0^-}(3+2x)\bigg(\dfrac{1}{x^3}+5\bigg)$.
Nous savons que $\displaystyle\lim_{x\to 0^-}(-2+x)=-2$, et on a $\displaystyle\lim_{x\to 0^-}\dfrac{1}{x^3}=-\infty$, donc $\displaystyle\lim_{x\to 0^-}\bigg(\dfrac{1}{x^3}+5\bigg)=-\infty$.
On en déduit grâce aux propriétés opératoires du produit des limites que: $\displaystyle\lim_{x\to 0^-}(3+2x)\bigg(\dfrac{1}{x^3}+5\bigg)=-\infty$.
Limite d'un quotient de fonctions.
Soit $f(x)=(2+\dfrac{1}{x^3})$ pour tout $x>0$, et soit $g(x)=(3-\dfrac{2}{x})$ pour tout $x\geq 1$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(2+\dfrac{1}{x^3})}{(3-\dfrac{2}{x})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(2+\dfrac{1}{x^3})=2$ et $\displaystyle\lim_{x\to +\infty}(3-\dfrac{2}{x})=3$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(2+\dfrac{1}{x^3})}{(3-\dfrac{2}{x})}=\dfrac{2}{3}$.
Soit $f(x)=(-2+\dfrac{3}{x^2})$ pour tout $x>0$, et soit $g(x)=(n+5)$ pour tout $x\in\mathbb{R}$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(-2+\dfrac{3}{x^2})}{(x+5)}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(-2+\dfrac{3}{x^2})=-2$ et $\displaystyle\lim_{x\to +\infty}(x+5)=+\infty$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(-2+\dfrac{3}{x^2})}{(x+5)}=0$.
Soit $f(x)=(x+\dfrac{3}{x})$ pour tout $x\geq 1$, et soit $g(x)=(5+\dfrac{2}{x^2})$ pour tout $x\geq 1$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(x+\dfrac{3}{x})}{(5+\dfrac{2}{x^2})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(x+\dfrac{3}{x})=+\infty$ et $\displaystyle\lim_{x\to +\infty}(5+\dfrac{2}{x^2})=5$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(x+\dfrac{3}{x})}{(5+\dfrac{2}{x^2})}=+\infty$.
Soit $f(x)=(2n-\dfrac{3}{x})$ pour tout $x\not=0$, et soit $g(x)=(-3+\dfrac{2}{x^2})$ pour tout $x\not=0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(2x-\dfrac{3}{x})}{(-3+\dfrac{2}{x^2})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(2x-\dfrac{3}{x})=+\infty$ et $\displaystyle\lim_{x\to +\infty}(-3+\dfrac{2}{x^2})=-3$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(2x-\dfrac{3}{x})}{(-3+\dfrac{2}{x^2})}=-\infty$.
Soit $f(x)=-x^2$ pour tout $x\in\mathbb{R}$, et soit $g(x)=(6+\dfrac{1}{x^2})$ pour tout $x\not=0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{-x^2}{(6+\dfrac{1}{x^2})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(-x^2)=-\infty$ et $\displaystyle\lim_{x\to +\infty}(6+\dfrac{1}{x^2})=6$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{-x^2}{(6+\dfrac{1}{x^2})}=-\infty$.
Soit $f(x)=-x^2$ pour tout $x\in\mathbb{R}$, et soit $g(x)=(-6+\dfrac{1}{x^2})$ pour tout $x\not=0$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{-x^2}{(-6+\dfrac{1}{x^2})}$.
Nous savons que $\displaystyle\lim_{x\to +\infty}(-x^2)=-\infty$ et $\displaystyle\lim_{x\to +\infty}(-6+\dfrac{1}{x^2})=-6$;
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{-x^2}{(-6+\dfrac{1}{x^2})}=+\infty$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(3+\dfrac{1}{x})}{-\dfrac{1}{x}-\dfrac{1}{x^2}}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} 3+\dfrac{1}{x}=3$ et $\displaystyle\lim_{x\to +\infty}(-\dfrac{1}{x}-\dfrac{1}{x^2})=0$. De plus pour tout $x>0$, il est clair que $-\dfrac{1}{x}-\dfrac{1}{x^2} < 0$, donc la fonction $g$ converge vers 0 tout en restant négative, on note cela: $\displaystyle\lim_{x\to +\infty}(-\dfrac{1}{x}-\dfrac{1}{x^2})=0^-$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(3+\dfrac{1}{x})}{(-\dfrac{1}{x}-\dfrac{1}{x^2})}=-\infty$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(-1+\dfrac{1}{x})}{\dfrac{1}{x}+\dfrac{1}{x^2}}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} (-1+\dfrac{1}{x})=-1$ et $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x}+\dfrac{1}{x^2})=0$. De plus pour tout $x>0$, il est clair que $\dfrac{1}{x}+\dfrac{1}{x^2}>0$, donc la fonction $g$ converge vers 0 tout en restant positive, on note cela: $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x}+\dfrac{1}{x^2})=0^+$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(-1+\dfrac{1}{x})}{(\dfrac{1}{x}+\dfrac{1}{x^2})}=-\infty$.
Calculons $\displaystyle\lim_{x\to +\infty}\dfrac{f(x)}{g(x)}=\displaystyle\lim_{x\to +\infty}\dfrac{(-1+\dfrac{1}{x})}{-\dfrac{2}{x}-\dfrac{1}{x^3}}$.
Nous savons que $\displaystyle\lim_{x\to +\infty} (-1+\dfrac{1}{x})=-1$ et $\displaystyle\lim_{x\to +\infty}(-\dfrac{2}{x}-\dfrac{1}{x^3})=0$. De plus pour tout $x>0$, il est clair que $-\dfrac{2}{x}-\dfrac{1}{x^3} < 0$, donc la fonction $g$ converge vers 0 tout en restant négative, on note cela: $\displaystyle\lim_{x\to +\infty}(\dfrac{1}{x}+\dfrac{1}{x^2})=0^-$.
On en déduit grâce aux propriétés opératoires du quotient des limites que: $\displaystyle\lim_{x\to +\infty}\dfrac{(-1+\dfrac{1}{x})}{(\dfrac{1}{x}+\dfrac{1}{x^2})}=+\infty$.
Exercice.
-
Déterminer les limites des fonctions suivantes au bornes du domaine de définition.
Théorème d'encadrement.
Soient $f, g, h$ trois fonctions définies sur un intervalle $I=[b,+\infty[$ et soit $l\in\mathbb{R}$.
Si pour tout $x\in I$, on a $g(x)\leq f(x)\leq h(x)$ et si $\displaystyle\lim_{x\to +\infty}g(x)=\displaystyle\lim_{x\to +\infty}h(x)=l$, alors $\displaystyle\lim_{x\to +\infty}f(x)=l$.
Donc pour tout $x\in[\eta;+\infty[$, on a $l-\epsilon < g(x)\leq f(x)\leq h(x) < l+\epsilon$, donc pour tout $x\in[\eta;+\infty[$, on a $l-\epsilon < f(x) < l+\epsilon$, ce qui veut dire que $\displaystyle\lim_{x\to +\infty}f(x)=l$.
Exemple.
Montrons que la fonction $j(x)=\dfrac{2x+\cos(x)}{3x-1}$ définie $]\dfrac{1}{3};+\infty[$ admet une limite en $+\infty$.Nous savons que pour tout $x\in\mathbb{R}$ $-1\leq\cos(x)\leq 1$. $\forall x\in\mathbb{R}$ $2x-1\leq 2x+\cos(x)\leq 2x+1$ or $\forall x\in]\frac{1}{3};+\infty[$ on a que $3x-1>0$ donc $\forall x\in]\dfrac{1}{3};+\infty[$ $\dfrac{2x-1}{3x-1}\leq\dfrac{2x+\cos(x)}{3x-1}\leq \dfrac{2x+1}{3x-1}$ On sait calculer $\displaystyle\lim_{x\to +\infty}\dfrac{2x-1}{3x-1}$ et $\displaystyle\lim_{x\to +\infty}\dfrac{2x+1}{3x-1}$ (Indétermination du type $\dfrac{\infty}{\infty}$). on a $\displaystyle\lim_{x\to +\infty}\frac{2x-1}{3x-1}=\dfrac{2}{3}$ et $\displaystyle\lim_{x\to +\infty}\frac{2x+1}{3x-1}=\dfrac{2}{3}$ donc nous avons $\displaystyle\lim_{x\to +\infty}\dfrac{2x+\cos(x)}{3x-1}=\dfrac{2}{3}$.
Exercice:
Soit la fonction $f$ définie sur $]0;+\infty[$, par $f(x)=\dfrac{\sin(x)}{x}$. Etudier la limite de la fonction $f$ en $+\infty$.
La fonction $g(x)=\cos(x)$, n'admet pas de limites, on ne peut donc pas utiliser les régles algébriques sur les limites.
Pour résoudre ce problème nous allons encadrer la fonction $f$, afin de pouvoir utiliser le théorème d'encadrement des limites, plus usuellement appélé, théorème des gendarmes.Pour tout $x\not=0$, on a: $-1\leq\sin(x)\leq 1$.
Puisque $x>0$, on a $-\dfrac{1}{x}\leq\dfrac{\sin(x)}{x}\leq\dfrac{1}{x}$.
Nous savons clairement que: $\displaystyle\lim_{x\to +\infty}\bigg(-\dfrac{1}{x}\bigg)=0$ et $\displaystyle\lim_{x\to +\infty}\dfrac{1}{x}=0$.
Donc d'après le théorème d'encadrement des limites, on peut conclure que $\displaystyle\lim_{x\to +\infty}\dfrac{\sin(x)}{x}=0$.
Théorème de comparaison.
Soient $f, g$ deux fonctions définies sur $I=]b;+\infty[$ ou $I=[b;+\infty[$.