Applications du produit scalaire.
Equations cartésiennes d'un plan.
- Soit $\overrightarrow{n}$ un vecteur non nul et $A$ un point de l'espace. L'unique plan passant par $A$ et de vecteur normal $\overrightarrow{n}$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}.\overrightarrow{n}=0$.
- Soit un plan $\mathcal{P}$ ayant pour vecteur normal $\overrightarrow{n}(a;b;c)\not=(0;0;0)$ alors le plan $\mathcal{P}$ a une équation cartésienne de la forme $ax+by+cz+d=0$;
- Réciproquement si $(a;b;c)\not=(0;0;0)$, l'ensemble des points $M(x;y;z)$ de l'espace tels que:
$ax+by+cz+d=0$ est un plan de vecteur normal $\overrightarrow{n}(a;b;c)$. - Le plan $\mathcal{P}:2x-5y+z-5=0$ a pour vecteur normal $\overrightarrow{n}=\begin{pmatrix}2\\-5\\1\\ \end{pmatrix}$.
- Le plan $\mathcal{P'}:-2x+5y-3z=9$ a pour vecteur normal $\overrightarrow{n}=\begin{pmatrix}-2\\5\\-3\\ \end{pmatrix}$.
- Considérons le plan $\mathcal{P}$ passant par $A(x_0;y_0;z_0)$ et de vecteur normal $\overrightarrow{n}=\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$ et $M(x;y;z)$un point quelconque de l'espace.
On sait que $\overrightarrow{AM}=\begin{pmatrix}x-x_0\\y-y_0\\z-z_0\\ \end{pmatrix}$.
Si $M(x;y;z)\in\mathcal{P}$ $\Leftrightarrow$ $\overrightarrow{AM}.\overrightarrow{n}=0$ $\Leftrightarrow$ $a(x-x_0)+b(y-y_0)+c(z-z_0)=0$ $\Leftrightarrow$ $ax+by+cz+(-ax_0-by_0-cz_0)=0$.
Posons $c=-ax_0-by_0-cz_0$, pour simplifier les notations.
Nous avons donc $M(x;y;z)\in\mathcal{P}$ $\Leftrightarrow$ $ax+by+cz+d=0$.
La relation reliant les coordonnées de $M$ entre elles $ax+by+cz+d=0$ s'appelle une équation cartésienne du plan $\mathcal{P}$. On note cela
$(\mathcal{P}):ax+by+cz+d=0$.Remarque.
Un plan $\mathcal{P}$ possède une infinité d'équations cartésiennes. En effet si $(\mathcal{P}):ax+by+cz+d=0$. - Réciproquement, Considérons l'ensemble $E$ des points $M(x;y;z)$ vérifiant la relation $ax+by+cz+d=0$.
Puisque$(a;b;c)\not=(0;0;0)$, on peut supposer par exemple que $a\not=0$. Donc le point $A(-\dfrac{d}{a};0;0)$ appartient à $E$. Donc l'ensemble $E$ n'est pas vide.
Pour garder le coté général de la démonstration, nous savons que $E$ contient un point $A$ dont on nommera les coordonées $(x_0;y_0;z_0)$. $M(x;y;z)$ appartient à $E$ $\Leftrightarrow$ $ax+by+cz+d=0=ax_0+by_0+cz_0+d$ $\Leftrightarrow$ $ax+by+cz+d=0=ax_0+by_0+cz_0+d$ $\Leftrightarrow$ $a(x-x_0)+b(y-y_0)+c(z-z_0)=0$.
Posons $\overrightarrow{n}=\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$ et $A(x_0;y_0;z_0)$.
Donc nous avons $M(x;y;z)$ appartient à $E$ $\Leftrightarrow$ $a(x-x_0)+b(y-y_0)+c(z-z_0)=0$ $\Leftrightarrow$ $\overrightarrow{AM}.\overrightarrow{n}=0$.
Donc $M$ appartient au plan passant par $A(x_0;y_0;z_0)$ et de vecteur normal $\overrightarrow{n}=\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$.
- Soit $M(x;y;z)$ un point de l'espace, on a $\overrightarrow{AM}=\begin{pmatrix}x+1\\y-3\\z-4\\ \end{pmatrix}$.
$M(x;y;z)\in\mathcal{P}$ $\Leftrightarrow$ $\overrightarrow{AM}.\overrightarrow{n}=0$ $\Leftrightarrow$ $(x+1)\times(-2)+(y-3)\times 1+(z-5)\times 5=0$ $\Leftrightarrow$ $-2x+y+5z-25=0$. - Comme $\overrightarrow{n}(-2;1;5)$ est un vecteur normal au plan $\mathcal{P}$,
nous savons d'après la réciproque du théorème précèdent que le plan $\mathcal{P}$ a pour équation:
$-2x+y+5z+d=0$. Or le point $A(-1;3;4)\in\mathcal{P}$; donc $-2\times (-1)+3+3\times 5+d=0$, donc $d=-25$.
Conclusion $(\mathcal{P}):$-2x+y+5z-25=0$. Distance d'un point à un plan.
- Soit $A$ un point de l'espace et $\mathcal{P}$ un plan. Le projeté orthogonal de $A$ sur $\mathcal{P}$ est le point d'intersection du plan $\mathcal{P}$ et de la droite passant par $A$ et perpendiculaire au plan $\mathcal{P}$.
- Soit $A$ un point de l'espace et $\mathcal{P}$ un plan.On définit la distance du point $A$ au plan $\mathcal{P}$, la distance $AH$ où $H$ est le projeté orthogonal de $A$ sur $\mathcal{P}$
Intersection de plans.
- Le vecteur $\overrightarrow{n}=\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$ est un vecteur directeur du plan $\mathcal{P}:ax+by+cz+d=0$.
- Le vecteur $\overrightarrow{n}=\begin{pmatrix}a'\\b'\\c'\\ \end{pmatrix}$ est un vecteur directeur du plan $\mathcal{P}:a'x+b'y+c'z+d'=0$.
- Les plans $\mathcal{P}$ et $\mathcal{P'}$ sont parallèles si et seulement si $\overrightarrow{n}(a;b;c)$ et $\overrightarrow{n'}(a';b';c')$ sont colinaires.
- Si $\overrightarrow{n}(a;b;c)$ et $\overrightarrow{n'}(a';b';c')$ ne sont pas colinaires alors les plans $\mathcal{P}$ et $\mathcal{P'}$ sont sécants, leur intersection est une droite.
- $(\mathcal{P_1}):2x-y+z-8=0$; $\overrightarrow{n_1}=\begin{pmatrix}2\\-1\\1\\ \end{pmatrix}$.
- $(\mathcal{P_2}):-4x+2y-2z+1=0$; $\overrightarrow{n_2}=\begin{pmatrix}-4\\2\\-2\\ \end{pmatrix}$.
- $(\mathcal{P_3}):6x-3y+3y=0$; $\overrightarrow{n_3}=\begin{pmatrix}6\\-3\\3\\ \end{pmatrix}$.
Etude de la position de deux plans.
- Soient $\mathcal{P}_1:x-2y+z=1$ et $\mathcal{P}_2:2x+y-3z-2=0$ deux plans.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont sécants. - Donner une représentation paramétriques de la droite $(d)$ intersection de $\mathcal{P}_1$ et $\mathcal{P}_2$.
Intersection d'une droite et d'un plan.
Proposition.
Soit $(d)$ une droite passant par un point $A$ de vecteur directeur $\overrightarrow{u}$ et soit $\mathcal{P}$ un plan de vecteur normal $\overrightarrow{n}$.
- Si $\overrightarrow{u}$ et $\overrightarrow{n}$ ne sont pas orthogonaux alors la droite $(d)$ et $\mathcal{P}$ sont sécants.
- Si $\overrightarrow{u}$ et $\overrightarrow{n}$ sont orthogonaux:
- Si $A$ appartient à $\mathcal{P}$, la droite (d) est incluse dans le plan $\mathcal{P}$.
- Si $A$ n'appartient pas à $\mathcal{P}$, la droite (d) est strictement parallèle au plan $\mathcal{P}$.
Configuration entre une droite $\Delta$ et un plan $\mathcal{P}$.
$\Delta$ et $\mathcal{P}$ sont sécants en un point $I$.
Exercice:
Soit $\mathcal{P}:x+y-2z-1=0$ le plan et $\mathcal{D}$ la droite de représentation paramétrique:
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=6-k \\y=-4+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.- Démontrer que la droite $\mathcal{D}$ est sécante au plan $\mathcal{P}$.
- Déterminer les coordonnées du point d'intersection de $\mathcal{D}$ et $\mathcal{P}$.
$\Delta$ est contenue dans $\mathcal{P}$.
Exercice:
Soit $\mathcal{P}:x+y-2z-1=0$ le plan et $\mathcal{D}$ la droite de représentation paramétrique:
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=1+k \\y=k\\z=k \\ \end{array}$ avec $k\in\mathbb{R}$.
Montrer que la droite $\mathcal{D}$ est incluse dans le plan $\mathcal{P}$.$\delta$ et $\mathcal{P}$ sont disjoints.
Exercice:
Soit $\mathcal{P}:x+y-2z-1=0$ le plan et $\mathcal{D}$ la droite de représentation paramétrique:
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=3+2s \\y=1+2s\\z=1+2s \\ \end{array}$ avec $s\in\mathbb{R}$.
Montrer que la droite $\mathcal{D}$ et le plan $\mathcal{P}$ sont disjoints.Détermination des angles d'un triangle quelconque dans l'espace.
- $a$, $b$, et $c$ les longueurs des côtés opposés aux sommets $A$, $B$, et $C$,
- $\widehat{A}$, $\widehat{B}$, et $\widehat{C}$ les mesures des angles associés aux sommets.
- $a^2=b^2+c^2-2bc\cos(\widehat{A})$.
- $b^2=a^2+c^2-2ac\cos(\widehat{B})$.
- $c^2=a^2+b^2-2ab\cos(\widehat{C})$.
- $cos(\widehat{A})=\dfrac{b^2+c^2-a^2}{2bc}$.
- $cos(\widehat{B})=\dfrac{a^2+c^2-b^2}{2ac}$.
- $cos(\widehat{C})=\dfrac{a^2+b^2-c^2}{2ab}$.
Théorème.
Exemple.
Déterminer une équation catésienne de plan.
Soit $A(-1;3;4)$ un point de l'espace et $\overrightarrow{n}(-2;1;5)$ un vecteur. Déterminer de deux façons différentes, une équation cartésienne du plan $\mathcal{P}$ passant par $A$ et de vecteur normal $\overrightarrow{n}$.
Définitions.
Théorème (En marge du programme).
Dans un repère orthonormé, la distance d'un point $A$ de coordonnées $(x_A;y_A;z_A)$ au plan $\mathcal{P}$ d'équation cartésienne $ax+by+cz+d=0$ est égale à:
$\dfrac{|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}.$
Donc nous avons $AH=\dfrac{|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}$.
Le vecteur $\overrightarrow{n}=\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$ est un vecteur directeur du plan $\mathcal{P}$ d'équation cartésienne $ax+by+cz+d=0$.
Les vecteurs $\overrightarrow{n}$ et $\overrightarrow{AH}$ sont colinéaires, donc $(\overrightarrow{n};\overrightarrow{AH})=0~~[pi]$, on en déduit que:
$\overrightarrow{n}.\overrightarrow{AH}$ $=||\overrightarrow{n}||\times AH\times \cos(\overrightarrow{n};\overrightarrow{AH})$ $=\sqrt{a^2+b^2+c^2}\times AH\times\cos(\overrightarrow{n};\overrightarrow{AH})$ et donc $|\overrightarrow{n}.\overrightarrow{AH}|=\sqrt{a^2+b^2+c^2}\times AH$.
Calculons le produit scalaire $\overrightarrow{n}.\overrightarrow{AH}$ d'un autre façon.
$\overrightarrow{n}.\overrightarrow{AH}$ $=a(x_H-x_A)+b(y_H-y_A)+c(z_H-z_A)$ $=ax_E+by_E+cy_E-ax_A-by_A-cz_A$.
Nous savons par définition que $H\in\mathcal{P}$, étant le projeté orthogonal de $A$ sur $\mathcal{P}$. Donc $ax_H+by_H+cz_H+d=0$, donc $ax_H+by_H+cz_H=-d$.
Nous en déduisons que $\overrightarrow{n}.\overrightarrow{AH}$ $=-d-ax_A-by_A-cz_A$ $=-(ax_A+by_A+cz_A+d)$.
Conclusion: $\sqrt{a^2+b^2+c^2}\times AH$ $=|-(ax_A+by_A+cz_A+d)|$ $=|-(ax_A+by_A+cz_A+d)|$.
On a: $AH=\dfrac{|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}$.
Les vecteurs $\overrightarrow{n}$ et $\overrightarrow{AH}$ sont colinéaires, donc $(\overrightarrow{n};\overrightarrow{AH})=0~~[pi]$, on en déduit que:
$\overrightarrow{n}.\overrightarrow{AH}$ $=||\overrightarrow{n}||\times AH\times \cos(\overrightarrow{n};\overrightarrow{AH})$ $=\sqrt{a^2+b^2+c^2}\times AH\times\cos(\overrightarrow{n};\overrightarrow{AH})$ et donc $|\overrightarrow{n}.\overrightarrow{AH}|=\sqrt{a^2+b^2+c^2}\times AH$.
Calculons le produit scalaire $\overrightarrow{n}.\overrightarrow{AH}$ d'un autre façon.
$\overrightarrow{n}.\overrightarrow{AH}$ $=a(x_H-x_A)+b(y_H-y_A)+c(z_H-z_A)$ $=ax_E+by_E+cy_E-ax_A-by_A-cz_A$.
Nous savons par définition que $H\in\mathcal{P}$, étant le projeté orthogonal de $A$ sur $\mathcal{P}$. Donc $ax_H+by_H+cz_H+d=0$, donc $ax_H+by_H+cz_H=-d$.
Nous en déduisons que $\overrightarrow{n}.\overrightarrow{AH}$ $=-d-ax_A-by_A-cz_A$ $=-(ax_A+by_A+cz_A+d)$.
Conclusion: $\sqrt{a^2+b^2+c^2}\times AH$ $=|-(ax_A+by_A+cz_A+d)|$ $=|-(ax_A+by_A+cz_A+d)|$.
On a: $AH=\dfrac{|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}$.
Plans perpendiculaires.
Dans un repère orthonormé, considérons deux plans $\mathcal{P}:ax+by+cz+d=0$ et $\mathcal{P'}:a'x+b'y+c'z+d=0$.
Les plans $\mathcal{P}$ et $\mathcal{P'}$ sont perpendiculaires si et seulement si $aa'+bb'+cc'=0$.
Démonstration:
Nous savons que:
Plans parallèles.
Dans un repère quelconque, considérons deux plans $\mathcal{P}:ax+by+cz+d=0$ et $\mathcal{P'}:a'x+b'y+c'z+d=0$.
Exemples:
Les trois vecteurs normaux sont colinéaires deux à deux.
Donc $(\mathcal{P_1})//(\mathcal{P_2})//(\mathcal{P_3})$.
Configuration entre deux plans.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont confondus.
Démontrer que les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont confondus.
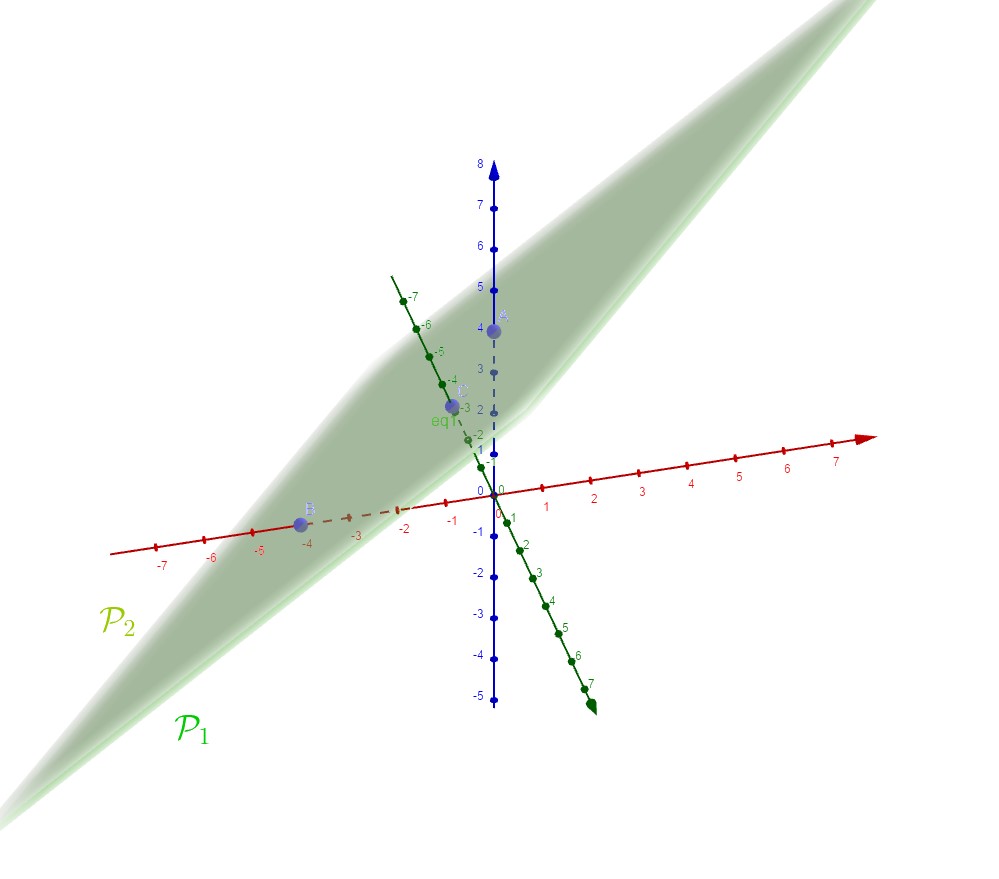
Exercice:
Soient $\mathcal{P}_1:2x-3y+z=3$ et $\mathcal{P}_2:-4x+6y-2z+6=0$ deux plans.Démontrer que les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont confondus.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont disjoints.
Démontrer que les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont stictements paralléles.
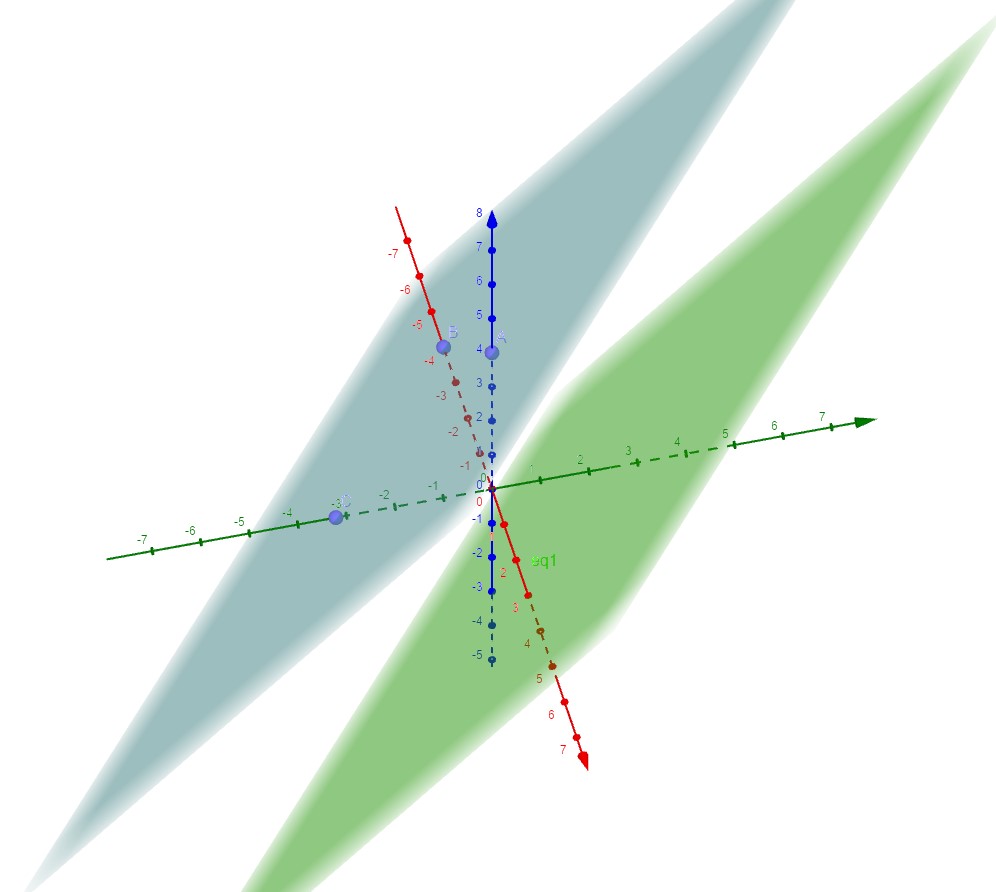
Exercice:
Soient $\mathcal{P}_1:2x-3y+z=3$ et $\mathcal{P}_2:-4x+6y-2z+7=0$ .Démontrer que les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ sont stictements paralléles.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont sécants.
Exercice:
Relation métrique d'un triangle dans l'espace.
-
Soit un triangle $ABC$ quelconque, on désigne par:
Remarque:
la démonstration de ces formules est la même que pour les relation métriques dans un triangle du plan. Revoir donc la leçon de première sur le produit scalaire du plan!