Combinatoire, dénombrements.
Cardinal d'ensembles.
- Soit $A$ un ensemble fini( constitué d'un nombre fini d'élément).
Le cardinal de $A$, noté $Card(A)$, est le nombre déléments de $A$. - Deux ensembles $A$ et $B$ sont disjoints lorsque $A\cap B=\emptyset$.
- Soient $A$ et $B$ deux ensembles non vides. Le produit cartésien de $A$ et $B$ est l'ensemble noté $A\times B$ (se lit $A$ croix $B$),
constitué des couples $(x;y)$ où $x$ est un élément de $A$ et $y$ un élément de $B$. Plus formellement on écrit:
$A\times B=\Bigg\{(x;y), x\in A~~~~ et~~~~ y\in B \Bigg\}$. - Cas Général:Soient $A_1$, $A_2$, ..., $A_n$, $n$ ensembles non vides.
Le produit cartésien $A_1\times A_2\times ...\times A_n$, est constitué des couples $(x_1;x_2;...;x_n)$ où $x_i$ est un élément de $A_i$ pour tout $1\leq i\leq n$.
Plus formellement on écrit:
$A_1\times A_2\times ...\times A_n=\Bigg\{(x_1;x_2;...;x_n)$, $\forall i\in\mathbb{N}$ tels que $1\leq i\leq n$ , $x_i\in A_i \Bigg\}$. - Soient $A$ et $B$ deux ensembles finis, alors: $Card(A\times B)=Card(A)\times Card(B)$.
- Cas Général: Soient $A_1$, $A_2$, ..., $A_n$, $n$ ensembles finis, alors:
$Card(A_1\times A_2\times...\times A_n)=Card(A_1)\times Card(A_2)\times...\times Card(A_n)=\Pi_{k=1}^n Card(A_k)$. Permutation d'un ensemble fini.
- Si $E=\{a\}$ il existe une seule permutation de $E$.
- Si $E=\{a,b\}$ il existe deux permutations de $E$: $\{a,b\}$, $\{b,a\}$.
- Si $E=\{a,b,c\}$, il existe 6 permutations de $E$: $\{a,b,c\}$, $\{a,c,b\}$, $\{b,a,c\}$, $\{b,c,a\}$, $\{c,a,b\}$, $\{c,b,a\}$.
- Il y a $n$ choix d'éléments possibles pour la
Case 1 - La première case étant complétée, il y a $(n-1)$ choix d'éléments possibles pour la
Case 2 - La première case et la deuxième case étant complétées, il y a $(n-2)$ choix d'éléments possibles pour la
Case 3 - ....etc....
- $n-3$ case sont déjà complétées, donc il reste $3$ choix possible pour la
Case n-2 - $n-2$ case sont déjà complétées, donc il reste $2$ choix possible pour la
Case n-1 - Il ne reste plus qu'un choix possible pour la
Case n Liste sans répétitions.
Exemples.
Soit $E=\{a,b,c,d\}$, par exemple si $p=2$, voici quelques exemples de listes de $2$ eléments sans répétition de $E$: $(a,b)$; $(c,d)$; $(a,c)$.
Proposition.
Soit $E$ un ensemble fini de cardinal $n\geq 1$, le nombre de listes sans répétitions de $p$ éléments de $E$, avec $1\leq p\leq n$, est
$\mathcal{A}_n^k=n\times(n-1)\times(n-2)\times...\times(n-(p-1))$.
Pour connaître le nombre de listes sans répétitions de $p$ éléments de $E$ il suffit de se demander de combien de façons possibles peut-on prendre et disposer d'élements de cette liste dans un tableau de $p$ cases.
Case 1 Case 2 Case 3 ... ... Case p-2 Case p-1 Case p - Il y a $n$ choix d'éléments possibles pour la
Case 1 - La première case étant complétée, il y a $(n-1)$ choix d'éléments possibles pour la
Case 2 - La première case et la deuxième case étant complétées, il y a $(n-2)$ choix d'éléments possibles pour la
Case 3 - ....etc....
- $p-3$ case sont déjà complétées, donc il reste $n-(p-3)$ choix possible pour la
Case p-2 - $p-2$ case sont déjà complétées, donc il reste $n-(p-2)$ choix possible pour la
Case p-1 - Il ne reste plus que $n-(p-1)$ choix possibles pour la
Case p
le nombre de listes sans répétitions de $p$ éléments de $E$, avec $1\leq p\leq n$, est:
$\mathcal{A}_n^k=n\times(n-1)\times(n-2)\times...\times(n-(p-1))$.- Il y a $n$ choix d'éléments possibles pour la
Liste avec répétitions.
Exemples.
Soit $E=\{a,b,c,d\}$, par exemple si $p=2$, voici quelques exemples de listes de $2$ éléments sans répétitions de $E$: $(a,a)$; $(c,d)$; $(c,c)$.
Proposition.
Soit $E$ un ensemble fini de cardinal $n\geq 1$, le nombre de listes avec répétitions de $p$ élèments de $E$, avec $p\geq 1$, est $n^p.$
Pour connaître le nombre de listes avec répétitions de $p$ éléments de $E$ il suffit de se demander de combien de façons possibles peut-on prendre et disposer d'élements de cette liste dans un tableau de $p$ cases. Sachant et c'est ce qui est vraiment important et différent de listes sans répétions, nous allons pouvoir prendre plusieurs fois le même élément de l'ensemble $E$.
Case 1 Case 2 Case 3 ... ... Case p-2 Case p-1 Case p
Pour chaque case du tableau nous avons $n$ choix possibles et comme il y a $p$ cases dans le tableau.
Le nombre de choix possibles est $\underbrace{n\times n\times...\times n}_{p~~ \mathrm{fois}}=n^p$.Conclusion: le nombre de listes avec répétitions de $p$ élèments de $E$, avec $p\geq 1$, est $n^p.$
Combinaisons.
- Soit $E=\{a,b,c,d\}$, prenons $p=2$, voici quelques exemples de 2-combinaisons de $E$: $\{a,c\}$; $\{d,a\}$; $\{a,d\}$; $\{b,c\}$.
- Il n'existe qu'une seule combinaison (partie) de $n$ éléments d'un ensemble $E$ de cardinal $n$, donc $\bigg( \begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)=1$, de même il existe $n$ parties (combinaisons) d'un seul élément d'un ensemble de cardinal $n$, donc on a $\bigg( \begin{array}[pos]{c} n\\ 1\\ \end{array}\bigg)=n$.
- Si $p>0$, Choisissons une partie $F$ de $p$ éléments d'un ensemble $E$ de cardinal $n$. Le nombre de permutations possibles de $F$ est $p!$.
Nous savons que:
$\bigg($nombre de partie à $p$ éléments de $E$ $\bigg)$$\times p!=$ nombre de listes sans répititions de $p$ éléments de de $E$.
C'est à dire, nous avons l'égalité:
$\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)\times p!=n\times(n-1)\times...\times(n-p+1)$. donc
$\bigg( \begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)=\dfrac{n(n-1)...(n-p+1)}{p!}=\dfrac{n!}{p!(n-p)!}$. - S p=0, il n'existe qu'une seule partie qui n'a pas d'éléments, c'est la partie $\emptyset$. Donc le nombre de parties de $E$ ayant 0 éléments est égal à 1.
On a donc: $\bigg(\begin{array}[pos]{c}n\\0\\\end{array}\bigg)=1$. Or $\dfrac{n!}{0!\times(n-0)!}=\dfrac{n!}{n!}=1$, la formule du théorème est aussi vérifiée pour $p=0$. - Pour tous entiers naturels $n$, on a: $\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)=1$.
- Pour tous entiers naturels $n$, on a: $\bigg(\begin{array}[pos]{c}n\\1\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array}\bigg)=n$.
- Pour tous entiers naturels $n$ et $p$ tel que $0\leq p\leq n$, on a: $\bigg(\begin{array}[pos]{c}n\\n-p\\ \end{array}\bigg)=\bigg( \begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$.
- Pour tous entiers naturels $n$ et $p$ tel que $0\leq p\leq n-1$, on a: $\bigg(\begin{array}[pos]{c}n-1\\p-1\\ \end{array}\bigg)$ $+\bigg( \begin{array}[pos]{c}n-1\\p\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$.
- $\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)=\dfrac{n!}{0!\times(n-0)!}=\dfrac{n!}{n!}=1$ et $\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)=\dfrac{n!}{n!\times(n-n)!}=1$.
- $\bigg(\begin{array}[pos]{c}n\\1\\ \end{array}\bigg)=\dfrac{n!}{1!\times(n-1)!}$ $=\dfrac{(n-1)!\times n}{(n-1)!}=n$.
$\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array}\bigg)=\dfrac{n!}{(n-1)!\times(n-(n-1))!}$ $=\dfrac{n!}{(n-1)!\times 1!}=n$. - $\bigg(\begin{array}[pos]{c}n\\n-p\\ \end{array}\bigg)=\dfrac{n!}{(n-p)!\times (n-(n-p))!}$ $=\dfrac{n!}{(n-p)!p!}=\bigg(\begin{array}[pos]{c}n\\p\\\end{array}\bigg)$
- $\bigg(\begin{array}[pos]{c}n-1\\p-1\\\end{array}\bigg)$ $+\bigg(\begin{array}[pos]{c}n-1\\p\\ \end{array}\bigg)$
$=\dfrac{(n-1)!}{(p-1)!((n-1)-(p-1))!}+\dfrac{(n-1)!}{p!((n-1)-p)!}$ $=\dfrac{(n-1)!}{(p-1)!((n-p)!}+\dfrac{(n-1)!}{p!((n-p-1)!}$.
Pour additionner les fractions précédentes il faut les mettre au même dénominateur c'est à dire $p!(n-p)!$, en effet on a:
$(p-1)!((n-p)! \times$p$=p!(n-p)!$ et $(p)!((n-p-1)! \times$(n-p)$=p!(n-p)!$.
Donc nous avons:
$\dfrac{(n-1)!}{(p-1)!((n-p)!}+\dfrac{(n-1)!}{p!((n-p-1)!}$ $=\dfrac{(n-1)!\times p}{(p-1)!((n-p)!\times p}+\dfrac{(n-1)!(n-p)}{p!((n-p-1)!(n-p)}$ $=\dfrac{(n-1)![p+(n-p)]}{p!(n-p)!}$ $=\dfrac{(n-1)!\times n}{p!(n-p)!}=\dfrac{n!}{p!(n-p)!}$ $=\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$.
En conclusion on a bien:
$\bigg(\begin{array}[pos]{c}n-1\\p-1\\ \end{array}\bigg)$ $+\bigg( \begin{array}[pos]{c}n-1\\p\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$. Formule du binôme de Newton.
Théorème.
Pour tous nombres complexes $a$ et $b$ et pour tout entier naturel $n\geq 1$, on a:
$(a+b)^n=\bigg( \begin{array}[pos]{c} n\\ 0\\ \end{array}\bigg)a^n+\bigg( \begin{array}[pos]{c} n\\ 1\\ \end{array}\bigg)a^{n-1}b+...+\bigg( \begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)a^{n-p}b^p+$ $...+\bigg( \begin{array}[pos]{c} n\\ n-1\\ \end{array}\bigg)ab^{n-1}+\bigg( \begin{array}[pos]{c} n\\ n\\ \end{array}\bigg)b^n$.
$(a-b)^n=\bigg( \begin{array}[pos]{c} n\\ 0\\ \end{array}\bigg)a^n-\bigg( \begin{array}[pos]{c} n\\ 1\\ \end{array}\bigg)a^{n-1}b+...+(-1)^p\bigg( \begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)a^{n-p}b^p+$ $...+(-1)^{n-1}\bigg( \begin{array}[pos]{c} n\\ n-1\\ \end{array}\bigg)ab^{n-1}+(-1)^n\bigg( \begin{array}[pos]{c} n\\ n\\ \end{array}\bigg)b^n$.Pour démontrer cette relation, nous allons faire un raisonnement par récurrence.
- Initialisation:Si $n=1$ on a $\bigg(\begin{array}[pos]{c} 1\\0\\ \end{array}\bigg)a^1b^0+\bigg(\begin{array}[pos]{c} 1\\0\\ \end{array}\bigg)a^0b^1$ $=a+b$ $=(a+b)^1$, la propriété est vraie au rang 1.
- Transmission:Supposons qu'il existe un entier $n\in\mathbb{N}$ tel que
$(a+b)^n=\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^n+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array}
\bigg)a^{n-1}b+...+\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n-p}b^p+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array}
\bigg)ab^{n-1}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)b^n$.
$(a+b)^{n+1}=(a+b)\times(a+b)^n$ $=\Bigg(\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^n+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array} \bigg)a^{n-1}b+...+\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n-p}b^p+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array} \bigg)ab^{n-1}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)b^n\Bigg)(a+b)$.
Donc en développant nous avons:
$\Bigg[\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^{n+1}+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array} \bigg)a^{n}b+...+$$\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n+1-p}b^p$ $+\bigg(\begin{array}[pos]{c}n\\p+1\\ \end{array}\bigg)a^{n-p}b^{p+1}+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array} \bigg)a^2b^{n-1}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)ab^n\Bigg]$ $+\Bigg[\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^{n}b+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array} \bigg)a^{n-1}b^2+...+$ $\bigg(\begin{array}[pos]{c}n\\p-1\\ \end{array}\bigg)a^{n-(p-1)}b^{p}$ $+ \bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n-p}b^{p+1}+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array} \bigg)ab^{n}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)b^{n+1}\Bigg]$.
Regroupons les termes, en remarquant que pour tout p on $n+1-p=n-(p-1)$.
$\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^{n+1}+\Bigg(\bigg(\begin{array}[pos]{c}n\\1\\ \end{array} \bigg)+\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)\Bigg)a^nb+...+ $ $\Bigg(\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)+\bigg(\begin{array}[pos]{c}n\\p-1\\ \end{array}\bigg)\Bigg)a^{n+1-p}b^p$ $+\Bigg(\bigg(\begin{array}[pos]{c}n\\p+1\\ \end{array}\bigg)+\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)\Bigg)a^{n-p}b^{p+1}+...+ \Bigg(\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)+\bigg(\begin{array}[pos]{c}n\\n-1\\\end{array}\bigg)\Bigg)ab^n+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)b^{n+1}$
Or nous saons que:- Pour tous entiers naturels $n$, on a: $\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n+1\\0\\ \end{array}\bigg)=1$ et $\bigg(\begin{array}[pos]{c}n\\n\\\end{array}\bigg)=\bigg(\begin{array}[pos]{c}n+1\\n+1\\ \end{array}\bigg)=1$.
- Pour tous entiers naturels $n$, on a: $\bigg(\begin{array}[pos]{c}n\\1\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array}\bigg)=n$.
- Pour tous entiers naturels $n$ et $p$ tel que $0\leq p\leq n$, on a: $\bigg(\begin{array}[pos]{c}n\\n-p\\ \end{array}\bigg)=\bigg( \begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$.
- Pour tous entiers naturels $n$ et $p$ tel que $0\leq p\leq n-1$, on a: $\bigg(\begin{array}[pos]{c}n-1\\p-1\\ \end{array}\bigg)$ $+\bigg( \begin{array}[pos]{c}n-1\\p\\ \end{array}\bigg)$ $=\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)$.
Donc en utilisant toute ces relations on obtient:
$(a+b)^{n+1}$ $=\bigg(\begin{array}[pos]{c}n+1\\0\\ \end{array}\bigg)a^{n+1}+\bigg(\begin{array}[pos]{c}n+1\\1\\ \end{array} \bigg)a^{n}b+...+\bigg(\begin{array}[pos]{c}n+1\\p\\ \end{array}\bigg)a^{n+1-p}b^p+...+\bigg(\begin{array}[pos]{c}n+1\\n\\ \end{array} \bigg)ab^{n}+\bigg(\begin{array}[pos]{c}n+1\\n+1\\ \end{array}\bigg)b^{n+1}$.
La propriété est donc transmise au rang $n+1$. - Conclusion: Pour tout $n\in\mathbb{N}$ la relation du binome de Newton est vérifiée.
- Puisque nous avons $(a+b)^n=\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^n+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array}
\bigg)a^{n-1}b+...+\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n-p}b^p+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array}
\bigg)ab^{n-1}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)b^n$ pour tout $a$ et $b$.
Nous avons $(a-b)^n=(a+(-b))^n$ $=\bigg(\begin{array}[pos]{c}n\\0\\ \end{array}\bigg)a^n+\bigg(\begin{array}[pos]{c}n\\1\\ \end{array} \bigg)a^{n-1}(-b)+...+\bigg(\begin{array}[pos]{c}n\\p\\ \end{array}\bigg)a^{n-p}(-b)^p+...+\bigg(\begin{array}[pos]{c}n\\n-1\\ \end{array} \bigg)a(-b)^{n-1}+\bigg(\begin{array}[pos]{c}n\\n\\ \end{array}\bigg)(-b)^n$.
Puisque $(-b)^p=(-1)^p\times b^p$ et $(-1)^p=1$ si $p$ est pair et $(-1)^p=-1$ si p est impair.
On a bien la relation:
$(a-b)^n=\bigg( \begin{array}[pos]{c} n\\ 0\\ \end{array}\bigg)a^n-\bigg( \begin{array}[pos]{c} n\\ 1\\ \end{array}\bigg)a^{n-1}b+...+(-1)^p\bigg( \begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)a^{n-p}b^p+$ $...+(-1)^{n-1}\bigg( \begin{array}[pos]{c} n\\ n-1\\ \end{array}\bigg)ab^{n-1}+(-1)^n\bigg( \begin{array}[pos]{c} n\\ n\\ \end{array}\bigg)b^n$.
Calcul de $(a+b)^n$ pour $n\leq16$.
Entrer la valeur de l' exposant $n$:
Réunions disjointes d'ensembles.
Proposition.
Soient $A_1$, $A_2$, ..., $A_n$ $n$ ensembles finis deux à deux disjoints, alors:
$Card(A_1\cup A_2\cup ...\cup A_n)=Card(A_1)+Card(A_2)+...+Card(A_n)=\Sigma_{k=1}^n A_k$.
Produit cartésien d'ensembles.
Exemple.
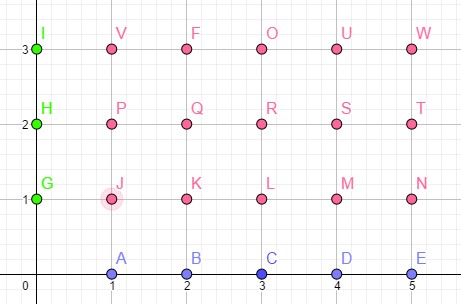
Par exemple Soit deux ensembles finis $X=\bigg\{A;B;C;D;E\bigg\}$ et $Y=\bigg\{G;H;I\bigg\}$.
La théorie des ensemble nous dit que:
$X\times Y$ $=\Bigg\{(A,G);(A,H),(A,I);(B,G);(B,H),(B,I);(C,G)$ $;(C,H);(C,I);(D,G);(D,H)$ $D,I);(E,G);(E,H),(E,I)\Bigg\}$
Interprétation graphique.
L'ensemble $X\times Y$ peut se voir comme des points du plan.Donc on a $X\times Y$ $=\Bigg\{J;K;L;M;N;P;Q;R;S;T;V;F;O;U;W\bigg\}$. On remarque que $Card(X\times Y)=15=5\times3$ $=Card(X)\times Card(Y)$.
Remarque.
L'ensemble des points du plan correspond à l'ensemble $\mathbb{R}\times\mathbb{R}=\mathbb{R}^2$.
L'ensemble des points de l'espace correspond à l'ensemble $\mathbb{R}\times\mathbb{R}\times\mathbb{R}=\mathbb{R}^3$.
Exercice:
Donner une représentation graphique de l'ensembe $X=\bigg\{1;2\bigg\}\times\bigg\{2;3;4\bigg\}\times\bigg\{1;2\bigg\}$.
Proposition.
Définition.
Une permutation d'un ensemble fini $E$ de cardinal $n$ est une liste ordonnée des $n$ éléments de $E$.
Eexemples:
Cas général, nombre de permutations d'un ensemble de cardinal $n$.
Remarque.
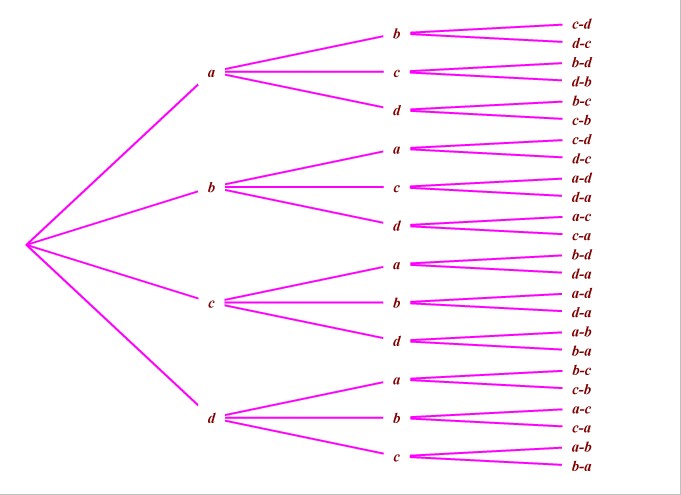
Si $E$ a pour cardinal un entier grand, il est difficile de trouver toutes les permutations de $E$, sans utiliser un arbre.
Combien y-a-t-il de permutations de $E=\{a,b,c,d\}$, pour répondre à cette question on peut construire un arbre , mais en construisant un arbre; on fait plus que de donner le nombre de permutations, on les énumère toutes.
Pour donner une permutation de $E$ il faut d'abord choisir la première lettre parmi les quatre données, puis il faut choisir la deuxième parmi les trois restantes,la troisième parmi les deux dernières, et la quatrième est la dernière lettre pas encore choisie.
Le nombre de possibilités pour faire une permutation de $E=\{a,b,c,d\}$ est donc $4\times 3\times 2\times 1=24$.
Proposition.
Le nombre de permutations d'un ensemble de $n$ éléments $(n\geq 1)$, est égal à:
$n\times(n-1)\times(n-2)\times...\times2\times 1$.
On note ce nombre $n!$ et on lit "n factoriel", par convention on pose $0!=1$.
Pour connaître le nombre de permutations d'un liste de $n$ éléments il suffit de se demander de combien de façons possibles peut-on prendre et disposer d'élements de cette liste dans un tableau de $n$ cases.
| Case 1 | Case 2 | Case 3 | ... | ... | Case n-2 | Case n-1 | Case n |
Le nombre de permutations d'un ensemble de $n$ éléments $(n\geq 1)$, est égal à:
$n\times(n-1)\times(n-2)\times...\times2\times 1=n!$.
Définition.
$E$ est un ensemble de $n$ éléments et $p$ un entier tel que $0\leq p\leq n$.
Une combinaison de $p$ éléments de $E$ est un sous-ensemble (ou partie) de $E$ qui contient $p$ éléments.
Le nombre de combinaisons (ou parties) de $p$ éléments d'un ensemble $E$ de cardinal $n$ est noté $\bigg(
\begin{array}[pos]{c}
n\\
p\\
\end{array}\bigg)$ et se lit "$p$ parmi $n$".
Exemples.
Remarque.
Il ne faut pas confondre une liste sans répétitions de $p$ éléments de $E$ et une combinaison de $p$ éléments de $E$, en effet si on prend comme le même exemple que précédemment $E=\{a,b,c,d\}$, avec $p=2$,$\{d,a\};~~\{a,d\}$ sont deux listes différentes car l'ordre des lettres est différent, par contre $\{d,a\}$; $\{a,d\}$ représente une même combinaison de deux éléments de $E$.Proposition.
Pour tout entier $n\geq 1$ et pour tout entier $p$ tel que $0\leq p\leq n$, on a:
$\bigg(
\begin{array}[pos]{c}
n\\
p\\
\end{array}\bigg)=\dfrac{n(n-1)...(n-p+1)}{p!}=\dfrac{n!}{p!(n-p)!}$.
-
Soit $E$ un ensemble fini de cardinal $n$, recherchons le nombre possible de sous-ensemble $F$ de cardinal $p$ de $E$.
Formules reliant les nombres $\bigg(\begin{array}[pos]{c} n\\ p\\ \end{array}\bigg)$.
Triangle de Pascal.
| n\p | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | ||||||||||
| 1 | 1 | 1 | |||||||||
| 2 | 1 | 2 | 1 | ||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |