Dérivation et convexité.
Rappels: Nombre dérivé. Fonction dérivée.
- Soit $f$ une fonction et $a$ un point intérieur à $\mathcal{D}_f$.
Dire que $f$ est dérivable en $a$, signifie qu'il existe un nombre réel $l$ tel que: $\displaystyle\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=l$.
Ce qui revient à dire aussi: $\displaystyle\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=l$.- Le nombre $l$ s'appelle le nombre dérivé de $f$ en $a$, on note $l=f^{'}(a)$.
- Lorsque $f$ est dérivable pour tout $x\in I$, avec $I\subset\mathcal{D}_f$ un intervalle inclu dans le domaine de $f$, on dit que $f$ est dérivable sur $I$.
- Si $f$ est une fonction dérivable sur $I\subset\mathcal{D}_f$,
la fonction dérivée de $f$ sur $I$ est la fonction notée $f^{'}$ qui à tout $x\in I$ associe le nombre réel $f^{'}(x)$.
$f^{'}:x\to f^{'}(x)$. Dérivées des fonctions usuelles.
- Soient $u$ et $v$ deux fonctions dérivables sur $I\subset\mathcal{D}_f$, et soit $\alpha\in\mathbb{R}$.
Alors $u+v$, $u-v$, $uv$, et $\alpha u$ sont dérivables sur $I$, et on a:- $(u+v)^{'}=u^{'}+v^{'}$ $~~~~~~~~~~~~~~$ $(u-v)^{'}=u^{'}-v^{'}$.
- $(uv)^{'}=u^{'}v+uv^{'}$ $~~~~~~~~~~~~~~$ $(\alpha u)^{'}=\alpha u^{'}$.
- Si de plus, $v$ ne s'annule pas sur $I$, alors $\frac{1}{v}$ et $\frac{u}{v}$ sont dérivables sur $I$ et:
- $\bigg(\dfrac{1}{v}\bigg)^{'}=-\dfrac{v^{'}}{v^2}$
- $\bigg(\dfrac{u}{v}\bigg)^{'}=\dfrac{u^{'}v-uv^{'}}{v^2}$
Applications de la dérivation.
- Si $f^{'}>0$ sur $I$, sauf peut-être en un nombre fini de points où $f^{'}$ s'annule , alors $f$ est strictement croissante sur $I$.
- Si $f^{'} < 0$ sur $I$, sauf peut-être en un nombre fini de points où $f^{'}$ s'annule , alors $f$ est strictement décroissante sur $I$.
- Si $f^{'}=0$ sur $I$, alors $f$ est constante sur $I$.
- Soit $f:I\to\mathbb{R}$ et $c\in I$, dire que $f(c)$ est un maximum local de $f$ en $c$ signifie qu'il existe un intervalle ouvert $J$ contenant $c$ tel que pour tout $x\in J\subset I$, $f(x)\leq f(c)$.
- Soit $f:I\to\mathbb{R}$ et $c\in I$, dire que $f(c)$ est un minimum local de $f$ en $c$ signifie qu'il existe un intervalle ouvert $J$ contenant $c$ tel que pour tout $x\in J\subset I$, $f(x)\geq f(c)$.
- Un extremum local est soit un maximum local, soit un minimum local.
- Si $f(c)$ est un extremum local, alors $f^{'}(c)=0$.
- Si $f^{'}(c)=0$ et si $f^{'}$ change de signe, alors $f(c)$ est un extremum local.
- Détermination de l'ensemble de définition de $f$ ($\mathcal{D}_f$).
- Etude des limites de $f$ aux bornes de $\mathcal{D}_f$.
- Etude du domaine de dérivation, calcul de la fonction dérivée, étude des variations de $f$.
- Détermination des asymptotes verticales, horizontales. Position relative de $\mathcal{C}_f$ par rapport aux asymptotes.
- Tracer la courbe représentative de $f$.
- Détermination du domaine de définition de $f$.
le nombre $f(x)=\dfrac{x}{x^2-1}$ existe si et seulement si $x^2-1\not=0$.
Résolvons l'équation $x^2-1=0$ $\Leftrightarrow$ $x^2=1$ $\Leftrightarrow$ $x=1$ ou $x=-1$.
Nous en déduisons que le domaine de définition de $f$ est $\mathbb{R}-\{-1;1\}$. On note cela $\mathcal{D}_f=\mathbb{R}-\{-1;1\}$. - Etude des limites de $f$ au bornes du domaine $\mathcal{D}_f=\mathbb{R}-\{-1;1\}$.
- En $+\infty$, calculons $\displaystyle\lim_{x\to+\infty}f(x)$. Nous sommes en présence d'une forme indéterminée du type $\dfrac{\infty}{\infty}$.
$f(x)=\dfrac{x}{x^2-1}$ $=\dfrac{x}{x\times(x-\dfrac{1}{x})}=\dfrac{1}{x-\dfrac{1}{x}}$. Nous savons que $\displaystyle\lim_{x\to+\infty}\dfrac{1}{x}=0$, on en déduit que $\displaystyle\lim_{x\to+\infty}(x-\dfrac{1}{x})=+\infty$.
Donc $\displaystyle\lim_{x\to+\infty}f(x)=0$. - En $-\infty$, on a $\displaystyle\lim_{x\to-\infty}\dfrac{1}{x}=0$, on en déduit que $\displaystyle\lim_{x\to+\infty}(x-\dfrac{1}{x})=-\infty$.
Donc $\displaystyle\lim_{x\to-\infty}f(x)=0$. - En $-1^+$, et en $-1^-$. Comme $\displaystyle\lim_{x\to -1}(x^2-1)=0$, nous devons étudier le signe de l'expression $x^2-1$.
$\displaystyle\lim_{x\to -1^-}x=\displaystyle\lim_{x\to -1^+}x=\displaystyle\lim_{x\to -1}x=-1$ et $\displaystyle\lim_{x\to -1^-}(x^2-1)=0^+$.Nous savons que $x^2-1=(x-1)(x+1)$.
Il est facile avec un tableau de signes d'avoir le signe de $x^2-1$.
$x-1=0$ $\Leftrightarrow$ $x=1$.
$x+1=0$ $\Leftrightarrow$ $x=-1$.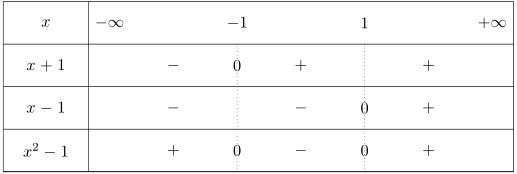
Donc $\displaystyle\lim_{x\to -1^-}\dfrac{x}{x^2-1}=-\infty$.
Nous savons que $\displaystyle\lim_{x\to -1^+}(x^2-1)=0^-$, donc $\displaystyle\lim_{x\to -1^+}\dfrac{x}{x^2-1}=+\infty$. - En $1^+$, et en $1^-$. Comme $\displaystyle\lim_{x\to 1}(x^2-1)=0$, nous devons étudier le signe de l'expression $x^2-1$, heureusement le travail a été fait pour $-1$.
$\displaystyle\lim_{x\to 1^-}x=\displaystyle\lim_{x\to 1^+}x=\displaystyle\lim_{x\to1}x=1$ et $\displaystyle\lim_{x\to 1^-}(x^2-1)=0^-$.
Donc $\displaystyle\lim_{x\to 1^-}\dfrac{x}{x^2-1}=-\infty$.
Nous savons que $\displaystyle\lim_{x\to 1^+}(x^2-1)=0^+$, donc $\displaystyle\lim_{x\to 1^+}\dfrac{x}{x^2-1}=+\infty$.
- En $+\infty$, calculons $\displaystyle\lim_{x\to+\infty}f(x)$. Nous sommes en présence d'une forme indéterminée du type $\dfrac{\infty}{\infty}$.
- Etude du domaine de dérivation, calcul de la fonction dérivée, étude des variations de $f$.
les fonctions $x\mapsto x$ et $x\mapsto x^2-1$ sont dérivables sur $\mathbb{R}$ et $x^2-1\not=0$, pour tout $x\in\mathbb{R}-\{-1;1\}$.
Donc la fonction $f(x)=\dfrac{x}{x^2-1}$ est dérivable sur $\mathcal{D}_f=\mathbb{R}-\{-1;1\}$.
Pour tout $x\in\mathbb{R}-\{-1;1\}$, on a $f^{'}(x)=\dfrac{1\times(x^2-1)-x\times(2x)}{(x^2-1)^2}$ $=\dfrac{-x^2-1}{(x^2-1)^2}$ $=-\dfrac{x^2+1}{(x^2-1)^2}$.
Pour tout $x\in\mathbb{R}-\{-1;1\}$, on a $x^2+1>0$ et $(x^2-1)^2>0$, donc $f^{'}(x)=-\dfrac{x^2+1}{(x^2-1)^2} < 0$. Nous avons donc le tableau de variations de $f$, ci-contre.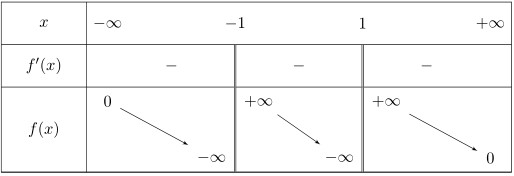
- Détermination des asymptotes verticales, horizontales. Position relative de $\mathcal{C}_f$ par rapport aux asymptotes.
- La droite $y=0$ est asymptote horizontale à la courbe de $f$ au voisinage de $+\infty$ et $-\infty$.
- Les droites $x=-1$ et $x=1$ sont des asymptotes verticales.
- Représentation de $\mathcal{C}_f$.
Dérivée d'une composée de fonctions.
- $x\in\mathcal{D}_f$,
- $f(x)\in\mathcal{D}_g$.
- Prouvons d'abord ceci en supposant que pour tout $x$ d'un voisinage de $a$ et différent de $a$ on ait $f(x)\not=f(a)$.
Puisque pour $x$ assez proche de $a$ on a $f(x)\not=f(a)$, on peut écrire: $T(x)=\dfrac{g\circ f(x)-g\circ f(a)}{f(x)-f(a)}\times\dfrac{f(x)-f(a)}{x-a}$.
Or $f$ est dérivable en $a\in I$, donc $\displaystyle\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}=f^{'}(a)$. Etudions la limite de $\dfrac{g\circ f(x)-g\circ f(a)}{f(x)-f(a)}$ quand $x$ tend vers $a$, on pose:
$h(x)=\dfrac{g\circ f(x)-g\circ f(a)}{f(x)-f(a)}$ et $k(X)=\dfrac{g(X)-g\circ f(a)}{X-f(a)}$. On remarque que $h(x)=k[f(x)]=k\circ f(x)$.
On sait que nous avons:- $f$ est dérivable en $a\in I$ donc continue en $a$ et donc $\displaystyle\lim_{x\to a}f(x)=f(a)$.
- $g$ est dérivable en $b=f(a)\in J$ donc $\lim_{X\to b}\dfrac{g(X)-g\circ f(a)}{X-f(a)}=g^{'}(b)=g^{'}(f(a))$.
Donc $\lim_{x\to a}T(x)=\lim_{x\to a}\dfrac{g\circ f(x)-g\circ f(a)}{f(x)-f(a)}\times\dfrac{f(x)-f(a)}{x-a}$ $=\lim_{x\to a}\dfrac{g\circ f(x)-g\circ f(a)}{f(x)-f(a)}\times\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}$ $=g^{'}[f(a)]\times f^{'}(a)$.
- Donnons la preuve du théorème quand pour tout $x$ appartenant à un voisinage de $a$ nous avons $f(x)=f(a)$, c'est à dire $f$ est localement constante.\newline Si $f$ est localement constante en $a$, alors il en est de même de $g\circ f$ en $a$, donc nous avons simultanément $f^{'}(a)=0$ et $(g\circ f)^{'}(a)=0$. Donc nous avons la relation $(g\circ f)^{'}(a)=g^{'}[f(a)]\times f^{'}(a)$. verifiée puisque $0=g^{'}[f(a)]\times 0$.
- $f(x)=e^{(x^3+x^2)}$ pour tout $x\in\mathbb{R}$.
- $f(x)=\ln(5x+3)$ pour tout $x\in]\frac{-3}{5};+\infty[$.
- Pour tout $x\in\mathbb{R}$, $f(x)=e^{(x^3+x^2)}=u\circ v(x)$, avec $u(x)=exp(x)$ et $v(x)=x^3+x^2$.
Les fonctions $u$ et $v$ sont dérivable sur $\mathbb{R}$, donc la fonction $f=u\circ v$ est aussi dérivable sur $\mathbb{R}$, nous avons:
$f^{'}(x)=u^{'}[v(x)]\times v^{'}(x)$ $=exp(x^3+x^2)\times(3x^2+2x)$ $=(3x^2+2x)e^{(x^3+x^2)}$.
Si vous désirez voir la leçon sur la fonction exponentielle.
- Pour tout $x\in]\frac{-3}{5};+\infty[$, $f(x)=\ln(5x+3)=u\circ v(x)$, avec $u(x)=\ln(x)$ et $v(x)=5x+3$.
La fonction $x\mapsto\ln(x)$ est dérivable sur $]0;+\infty[$ et $v$ est dérivable sur $\mathbb{R}$ et pour tout $x\in]\frac{-3}{5};+\infty[$, $v(x)\in]0;+\infty[$.
Donc la fonction $f=u\circ v$ est aussi dérivable sur $]\frac{-3}{5};+\infty[$, nous avons, $u^{'}(y)=\dfrac{1}{y}$, pour tout $y>0$.
Donc $f^{'}(x)=u^{'}[v(x)]\times v^{'}(x)$ $=\dfrac{v^{'}(x)}{v(x)}$ $=\dfrac{5}{5x+3}$.
Si vous désirez voir la leçon sur la fonction logarithme.
Cas particuliers de dérivées de fonctions composées.
- $f(x)=\sqrt{x^2+1}$ pour tout $x\in\mathbb{R}$.
- $f(x)=\sqrt{3x-1}$ pour tout $x\in]\frac{1}{3};+\infty[$.
- $f(x)=\sqrt{\dfrac{x}{x-2}}$ pour tout $x\in]-\infty;0[\cup]2;+\infty[$.
- $f(x)=\sqrt{x^2+1}$ pour tout $x\in\mathbb{R}$.
Donc pour tout $x\in\mathbb{R}$, nous avons $f(x)=\sqrt{u(x)}$ avec $u(x)=x^2+1$.
Pour tout $x\in I=\mathbb{R}$, $u(x)>0$, donc comme la fonction $u$ est dérivable sur $\mathbb{R}$, on peut en déduire grâce au théorème que $f=\sqrt{u}$ est dérivable sur $\mathbb{R}$, nous avons:
$f'(x)=\dfrac{u^{'}(x)}{2\sqrt{u(x)}}$ $=\dfrac{2x}{2\sqrt{x^2+1}}$ $=\dfrac{x}{\sqrt{x^2+1}}$. - $f(x)=\sqrt{3x-1}$ pour tout $x\in]\frac{1}{3};+\infty[$.
Donc pour tout $x\in]\frac{1}{3};+\infty[$, nous avons $f(x)=\sqrt{u(x)}$ avec $u(x)=3x-1$.
Pour tout $x\in I=]\frac{1}{3};+\infty[$, $u(x)>0$, donc comme la fonction $u$ est dérivable sur $\mathbb{R}$, on peut en déduire grâce au théorème que $f=\sqrt{u}$ est dérivable sur $]\frac{1}{3};+\infty[$, nous avons:
$f'(x)=\dfrac{u^{'}(x)}{2\sqrt{u(x)}}$ $=\dfrac{3}{2\sqrt{3x-1}}$. - $f(x)=\sqrt{\dfrac{x}{x-2}}$ pour tout $x\in]-\infty;0[\cup]2;+\infty[$.
Donc pour tout $x\in]-\infty;0[\cup]2;+\infty[$, nous avons $f(x)=\sqrt{u(x)}$ avec $u(x)=\dfrac{x}{x-2}$.
Pour tout $x\in I=]-\infty;0[\cup]2;+\infty[$, $u(x)>0$, donc comme la fonction $u$ est dérivable sur $\mathbb{R}-\{2\}$, on peut en déduire grâce au théorème que $f=\sqrt{u}$ est dérivable sur $]-\infty;0[\cup]2;+\infty[$, nous avons:$f'(x)=\dfrac{u^{'}(x)}{2\sqrt{u(x)}}$.
Calculons $u'(x)$, on a $u'(x)=\dfrac{1\times(x-2)-x\times 1}{(x-2)^2}$ $=\dfrac{-2}{(x-2)^2}$ pour tout $x\not=2$.
Donc pour tout $x\in]-\infty;0[\cup]2;+\infty[$, on a $f'(x)=\dfrac{\dfrac{-2}{(x-2)^2}}{2\sqrt{\dfrac{x}{x-2}}}$ $=\dfrac{-1}{(x-2)^2}\times\dfrac{\sqrt{x-2}}{\sqrt{x}}$ $=\dfrac{-1}{(x-2)\sqrt{x-2}\sqrt{x}}$ $=\dfrac{-1}{(x-2)\sqrt{x(x-2)}}$. - Si $n\geq 1$, la fonction $f$ définie sur $I$ par $f(x)=[u(x)]^n$ est dérivable sur $I$ et pour tout $x\in I$ on a: $f^{'}(x)=n[u(x)]^{n-1}\times u^{'}(x)$.
- Si $n < -1$, et si de plus la fonction $u$ ne s'annule pas sur $I$, la fonction $f$ définie sur $I$ par $f(x)=[u(x)]^n$ est dérivable sur $I$ et pour tout $x\in I$ on a: $f^{'}(x)=n[u(x)]^{n-1}\times u^{'}(x)$.
- Soit $n\geq 1$, posons la fonction $f$ définie sur $I$ par $f(x)=[u(x)]^n$.
On peut remarquer que $f(x)=v\circ u(x)$, avec $v(x)=x^n$.
La fonction $v$ est dérivable sur $\mathbb{R}$, donc toutes les conditions d'utilisation du théorème sur la dérivation d'une fonction composée sont vérifiés.
On a donc $f'(x)=v'[u(x)]\times u'(x)$, or $v'(y)=ny^{n-1}$ pour tout $y\in\mathbb{R}$.
Donc $f^{'}(x)=n[u(x)]^{n-1}\times u^{'}(x)$. - Soit $n\geq 1$, posons la fonction $f$ définie sur $I$ par $f(x)=[u(x)]^n$. Supposons de plus que la fonction $u$ ne s'annule pas sur $I$.
On peut remarquer que $f(x)=v\circ u(x)$, avec $v(x)=x^n=\dfrac{1}{x^{-n}}$.
Nous savons que la fonction $v$ est dérivable sur $\mathbb{R}^\star$ et pour tout $x\in I$, $u(x)\not=0$. Les conditions du théorème sur la dérivation d'une fonction composée sont vérifiés.
On a donc $f'(x)=v'[u(x)]\times u'(x)$, or $v'(y)=ny^{n-1}$ pour tout $y\in\mathbb{R}^\star$ $(y\not=0)$.
Donc $f^{'}(x)=n[u(x)]^{n-1}\times u^{'}(x)$.Remarque.
Cela semble être la même formule que dans le cas $n\geq1$, mais dans le cas $n < -1$, l'expression $x^n$ désigne en fait la fraction $\dfrac{1}{x^{-n}}$.
Donc l'expression $f^{'}(x)=n[u(x)]^{n-1}\times u^{'}(x)$, n'est simplemnt qu'une reformulation de la formule suivante:
$f^{'}(x)=\dfrac{n\times u^{'}(x)}{[u(x)]^{1-n}}$. - $f(x)=(x^2+3x+5)^{12}$ pour tout $x\in\mathbb{R}$.
- $f(x)=\bigg(\dfrac{x}{x-2}\bigg)^5$ pour tout $x\in\mathbb{R}-\{2\}$.
- $f(x)=\dfrac{1}{(x^2+4)^6}$ pour tout $x\in\mathbb{R}$.
- $f(x)=(x^2+3x+5)^{12}$ pour tout $x\in\mathbb{R}$.
Donc pour tout $x\in\mathbb{R}$, nous avons $f(x)=(u(x))^{12}$ avec $u(x)=x^2+3x+5$.
La fonction $u$ est dérivable sur $\mathbb{R}$, on peut en déduire grâce au théorème que $f=u^{12}$ est dérivable sur $\mathbb{R}$, nous avons:
$f'(x)=12[u(x)]^{11}\times u^{'}(x)$ $=12(x^2+3x+5)^{11}\times(2x+3)$ $=12(2x+3)(x^2+3x+5)^{11}$. - $f(x)=\bigg(\dfrac{x}{x-2}\bigg)^5$ pour tout $x\in\mathbb{R}-\{2\}$.
Donc pour tout $x\in\mathbb{R}-\{2\}$, nous avons $f(x)=(u(x))^{5}$ avec $u(x)=\dfrac{x}{x-2}$.
La fonction $u$ est dérivable sur $\mathbb{R}-\{2\}$, et $u'(x)=\dfrac{1\times(x-2)-x\times 1}{(x-2)^2}$ $=\dfrac{-2}{(x-2)^2}$ pour tout $x\not=2$.
On peut en déduire grâce au théorème que $f=u^{5}$ est dérivable sur $\mathbb{R}-\{2\}$, nous avons:
$f'(x)=5[u(x)]^{4}\times u^{'}(x)$ $=5\bigg(\dfrac{x}{x-2}\bigg)^4\times\bigg(\dfrac{-2}{(x-2)^2}\bigg)$ $=\dfrac{-10x^4}{(x-2)^6}$. - $f(x)=\dfrac{1}{(x^2+4)^6}$ pour tout $x\in\mathbb{R}$.
On remarque tout d'abord que la fonction $f$ peut s'écrire comme une puissance négative de $u$. En effet, nous avons $f(x)=(x^2+4)^{-6}$ $=u(x)^{-6}$ avec $u(x)=x^2+4$.
Pour tout $x\in I=\mathbb{R}$, $u(x)\not=0$, donc comme la fonction $u$ est dérivable sur $\mathbb{R}$, on peut en déduire grâce au théorème que $f=u^{-6}$ est dérivable sur $\mathbb{R}$, nous avons:
Pour tout $x\in\mathbb{R}$, $f'(x)=(-6)[u(x)]^{-6-1}\times u^{'}(x)$ $=-6[u(x)]^{-7}\times u^{'}(x)$ $=-6(x^2+1)^{-7}\times(2x)$ $=\dfrac{-12x}{(x^2+1)^7}$. Dérivées successives.
- Soit $f$ une fonction dérivable sur $I\subset\mathbb{R}$ sa fonction dérivée $f^{'}$ se note ou parfois $f^{(1)}$, on dit auusi dérivée première.
- Si $f^{'}=f^{(1)}$ est dérivable sur $I$ la fonction dérivée de $f^{'}$ se note $f^{''}$ ou $f^{(2)}$, on appelle $f^{''}=f^{(2)}$ dérivée seconde (ou d'ordre 2) de $f$.
- Par itération, si ,pour un entier $n\in\mathbb{N}$ la fonction $f^{(n)}$ est dérivable sur $I$, on note par $f^{(n+1)}$ la fonction dérivée de la fonction $f^{(n)}$. On a pour tout $n\geq 2$:
$f^{(n+1)}=\big(f^{(n)}\big)^{'}$.
Remarque
En physique on note parfois pour tout $n\geq 2$ $f^{(n)}(x)=\dfrac{d^n f}{dx^n}(x)$. - $f'(x)=5x^4+4x^3+3x^2+10$.
- $f^{''}(x)=(5x^4+4x^3+3x^2+10)^{'}$ $=20x^3+12x^2+6x$.
- $f^{'''}(x)=(f^{''})^{'}(x)=60x^2+24x+6$.
- $f^{(4)}(x)=f^{(3)}(x)^{'}=120x+24$.
Convexité.
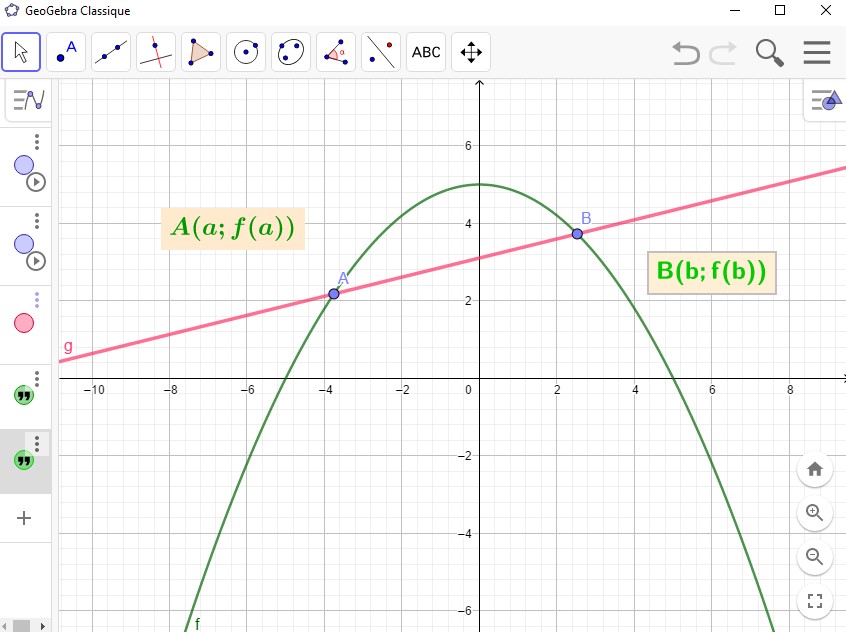
- Soit $f$ une fonction définie sur un intervalle $I$ et $\mathcal{C}_f$ sa courbe représentative dans un repère orthogonal.
On dit que $f$ est convexe sur $I$, lorsque pour tous points $A$ et $B$ distincts de la courbe $\mathcal{C}_f$, le segment $[AB]$ est au dessus de la courbe $\mathcal{C}_f$ entre $A$ et $B$. - Soit $f$ une fonction définie sur un intervalle $I$ et $\mathcal{C}_f$ sa courbe représentative dans un repère orthogonal.
On dit que $f$ est concave sur $I$, lorsque pour tous points $A$ et $B$ distincts de la courbe $\mathcal{C}_f$, le segment $[AB]$ est en dessous de la courbe $\mathcal{C}_f$ entre $A$ et $B$. - $f$ est convexe sur $I$ $\Leftrightarrow$ Pour tout $a\in I$, $b\in I$ et $t\in[0;1]$, on a: $f\bigg(ta+(1-t)b\bigg)\leq tf(a)+(1-t)f(b)$.
- $f$ est concave sur $I$ $\Leftrightarrow$ Pour tout $a\in I$, $b\in I$ et $t\in[0;1]$, on a: $f\bigg(ta+(1-t)b\bigg)\geq tf(a)+(1-t)f(b)$.
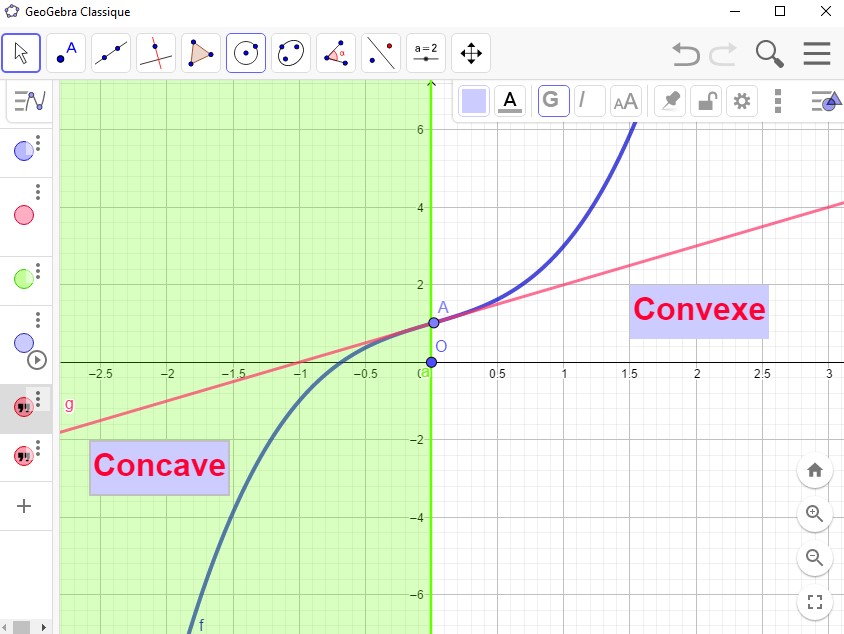
- La fonction $f$ est convexe sur $I$.
- La courbe représentative de $f$ est entièrement située au dessus de ses tangentes.
- La fonction $f^{'}$ est croissante sur l'intervalle $I$.
- $f''(x)\geq 0$ pour tout $x\in I$.
- Montrer que $g^{''}(x)=\dfrac{6}{(x-1)^3}$, pour tout $x\in\mathbb{R}-\{1\}$.
- Etudier le signe de $g^{''}(x)$, en déduire la convexité de $g$ sur $\mathbb{R}-\{1\}$.
- Pour tout $x\in\mathbb{R}-\{1\}$, on a $g'(x)=\dfrac{1\times(x-1)-(x+2)\times 1}{(x-1)^2}$ $=\dfrac{-3}{(x-1)^2}$ $=-3(x-1)^{-2}$.
Calculons $g^{''}(x)=\bigg[g'(x)\bigg]^{'}$ $=-3(u(x))^{-2}$, avec $u(x)=x-1$. Pour tout $x\in I=\mathbb{R}-\{1\}$, $u(x)\not=0$, donc comme la fonction $u$ est dérivable sur $\mathbb{R}$, on peut en déduire grâce au théorème que $f=(-3)u^{-2}$ est dérivable sur $\mathbb{R}-\{1\}$, nous avons:
Pour tout $x\in\mathbb{R}-\{1\}$, $f'(x)=(-3)\times(-2)[u(x)]^{-2-1}\times u^{'}(x)$ $=6[u(x)]^{-3}\times u^{'}(x)$ $=6(x-1)^{-3}\times(1)$ $=\dfrac{6}{(x-1)^3}$. - Etudions le signe de $g^{''}(x)=\dfrac{6}{(x-1)^3}$. Nous savons que $x$ et $x^3$ ont le même signe cours de seconde.
Donc on a: signe de $g^{''}(x)$ est égal au signe de $(x-1)$.
$x-1\geq 0$ $\Leftrightarrow$ $x\geq 1$, donc- $f$ est convexe sur $[1;+\infty[$.
- $f$ est concave sur $]-\infty;1]$.
Point d'inflexion d'une courbe de fonction.
- Déterminer la fonction dérivée seconde de $f$.
- Etudier le signe de $f^{''}(x)$.
- En déduire la convexité de $f$ et les abscisses des éventuels points d'inflexion.
- Pour tout $x\in\mathbb{R}$, $f'(x)=\dfrac{1}{4}\times 4x^3-3x^2+10$ $=x^3-3x^2+10$.
- Pour tout $x\in\mathbb{R}$, $f^{''}(x)=3x^2-6x=3x(x-2)$.
- $3x=0$ $\Leftrightarrow$ $x=0$
$x-2=0$ $\Leftrightarrow$ $x=2$.
Etudins le signe de $f^{''}(x)=3x(x-2)$, à laide du tableau de signes ci-contre.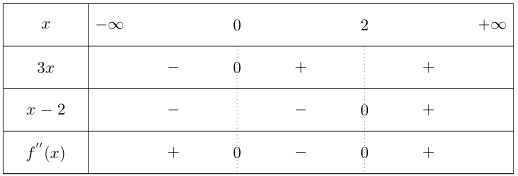
- $f^{''}(x)\geq 0$ pour tout $x\in]-\infty;0]\cup[2;+\infty[$ $\Leftrightarrow$ $f$ est convexe sur $]-\infty;0]\cup[2;+\infty[$.
- $f^{''}(x)\leq 0$ pour tout $x\in[0;2]$ $\Leftrightarrow$ $f$ est concave sur $[0;2]$.
- $f$ est convexe sur $I$ $\Leftrightarrow$ Pour tout $a\in I$, $b\in I$ et $t\in[0;1]$, on a: $f\bigg(ta+(1-t)b\bigg)\leq tf(a)+(1-t)f(b)$.
- $f$ est concave sur $I$ $\Leftrightarrow$ Pour tout $a\in I$, $b\in I$ et $t\in[0;1]$, on a: $f\bigg(ta+(1-t)b\bigg)\geq tf(a)+(1-t)f(b)$.
- Si on prend $t=\dfrac{1}{2}$, $1-t=\dfrac{1}{2}$, on a $f\bigg(\frac{1}{2}a+\frac{1}{2}b\bigg)\leq \dfrac{1}{2}f(a)+\dfrac{1}{2}f(b)$.
Donc, on obtient bien l'inégalité: $f\bigg(\dfrac{a+b}{2}\bigg)\leq\dfrac{f(a)+f(b)}{2}$. - Si on prend $t=\dfrac{1}{2}$, $1-t=\dfrac{1}{2}$, on a $f\bigg(\frac{1}{2}a+\frac{1}{2}b\bigg)\geq \dfrac{1}{2}f(a)+\dfrac{1}{2}f(b)$.
Donc, on obtient bien l'inégalité: $f\bigg(\dfrac{a+b}{2}\bigg)\geq\dfrac{f(a)+f(b)}{2}$. - Si $f$ est une fonction définie sur $I$ convexe alors, pour tout réels $a$ et $b$ de $I$, on a: $f\bigg(\dfrac{a+b}{2}\bigg)\leq\dfrac{f(a)+f(b)}{2}$.
- Si $f$ est une fonction définie sur $I$ concave alors, pour tout réels $a$ et $b$ de $I$, on a: $f\bigg(\dfrac{a+b}{2}\bigg)\geq\dfrac{f(a)+f(b)}{2}$.
Définitions.
Opérations sur les dérivées.
Dérivées des fonctions usuelles.
| Fonction $f$ | Dérivée $f^{'}$ | Domaine de dérivabilité de $f$ |
| $f(x)=k$ | $f^{'}(x)=0$ | $\mathbb{R}$ |
| $f(x)=x^n$ | $f^{'}(x)=nx^{n-1}$ | $\mathbb{R}$ si $n\geq 1$ et $\mathbb{R}^\star$ si $n\leq -1$ |
| $f(x)=\frac{1}{x}$ | $f^{'}(x)=-\frac{1}{x^2}$ | $\mathbb{R}^\star$ |
| $f(x)=\sqrt{x}$ | $f^{'}(x)=\frac{1}{2\sqrt{x}}$ | $]0;+\infty[$ |
| $f(x)=\sin{x}$ | $f^{'}(x)=\cos{x}$ | $\mathbb{R}$ |
| $f(x)=\cos{x}$ | $f^{'}(x)=-\sin{x}$ | $\mathbb{R}$ |
| $f(x)=\tan{x}$ | $f^{'}(x)=1+\tan{x}^2$ | $\mathbb{R}-\{\frac{\pi}{2}+k\pi; k\in\mathbb{Z}\}$ |
| $f(x)=|x|$ | $f^{'}(x)=1$ si $x>0$ et $f^{'}(x)=-1$ si $x < 0$ | $\mathbb{R}^\star$ |
Théorème.
Soit $f$ une fonction dérivable sur $I\subset\mathcal{D}_f$.
Définitions.
Théorème.
Soit $f$ une fonction dérivable sur un intervalle ouvert $I$, $c\in I$.
Plan d'étude d'une fonction.
Exemple d étude d'une fonction.
Etudier la fonction $f(x)=\dfrac{x}{x^2-1}$.
Composition de fonctions.
Soient $f$ et $g$ deux fonctions. la fonction qui à $x$ fait correspondre "quand cela est possible" le nombre réel $g[f(x)]$ se note $f\circ g$ (lire " g rond f" ). $f\circ g:x\mapsto g[f(x)]$.
Remarque:
L'écriture $g\circ f(x)=g[f(x)]$ n'a de sens que si $x\in\mathcal{D}_f$ et $f(x)\in\mathcal{D}_g$.Donc l'ensemble de définition de $g\circ f$ est constitué de tous les réels $x$ tels que:
Exemple:
Soient $f:x\to 2x+5$ et $g:x\to\sqrt{x}$, on sait que le domaine de définition de$f$ est $\mathbb{R}$,
et celui de $g$ est $\mathbb{R}^+$, on note cela $\mathcal{D}_f=\mathbb{R}$ et $\mathcal{D}_g=\mathbb{R}^+=[0;+\infty[$.
Regardons lorsque la valeur $g\circ f(x)$ est définie, nous avons
$g\circ f(x)=g[f(x)]=\sqrt{2x+5}$.
Pour que $g\circ f(x)$ soit définie il faut que $2x+5\geq 0$, c'est à dire $x\in[-\dfrac{5}{2};+\infty[$.
Donc nous avons $\mathcal{D}_{g\circ f}=[-\dfrac{5}{2};+\infty[$.
Exercice.
Soient $f$ et $g$ sont les fonctions définies par :$f(x)=\dfrac{x+3}{x+1}~~~~et~~~~g(x)=\dfrac{x}{x+2}$.
On pose $h=g\circ f$.
Trouver l'ensemble de définition de $h$ et calculer explicitement $h(x)$.
On sait que $\mathcal{D}_g=\mathbb{R}-\{-2\}$ et $\mathcal{D}_f=\mathbb{R}-\{-1\}$, pour que l'expression $g\circ f(x)$ soit définie il faut que $f(x)\not=-2$.
Résolvons l'équation $f(x)\not=-2$.
$\dfrac{x+3}{x+1}=-2$ $\Leftrightarrow$ $x+3=-2(x+1)$ $\Leftrightarrow$ $3x=-5$ $\Leftrightarrow$ $x=\dfrac{-5}{3}$
Donc $x\in\mathbb{R}-\{-1\}$ et $x\not=\dfrac{-5}{3}$, ce qui implique que
$\mathcal{D}_{g\circ f}=\mathbb{R}-\{\dfrac{-5}{3};-1\}$.
Calculons pour $x\in\mathbb{R}-\{\dfrac{-5}{3};-1\}$ l'expression $g\circ f(x)$.
$g\circ f(x)=\dfrac{\bigg(\dfrac{x+3}{x+1}\bigg)}{\bigg(\dfrac{x+3}{x+1}\bigg)+2}$
$=\dfrac{\bigg(\dfrac{x+3}{x+1}\bigg)}{\bigg(\dfrac{x+3}{x+1}\bigg)+2\times\bigg(\dfrac{x+1}{x+1}\bigg)}$
Donc $g\circ f(x)=\dfrac{\dfrac{x+3}{x+1}}{\dfrac{3x+5}{x+1}}$ $=\dfrac{x+3}{x+1}\times\dfrac{x+1}{3x+5}=\dfrac{x+1}{3x+5}$.
Dérivée d'une fonction composée.
Soit $g$ une fonction dérivable sur un intervalle $J$ et soit $f$ une fonction dérivable sur $I$ telle que pour tout $x\in I$ alors $f(x)\in J$.
Alors la fonction $g\circ f$ est dérivable sur $I$ et pour tout $x\in I$ on a: $(g\circ f)^{'}(x)=g^{'}[f(x)]\times f^{'}(x)$.
Exercice.
Calculer la fonction dérivée de $f$ sur l'intervalle $I$ donné:
Dérivation de $x\to\sqrt{u(x)}$.
Soit $u$ une fonction dérivable sur une partie $I$ de $\mathbb{R}$ telle que $u(x)>0$ pour tout $x\in I$.
Alors La fonction $f$ définie sur $I$ par $f(x)=\sqrt{u(x)}$ est dérivable sur $I$ et pour tout $x\in I$ on a: $f^{'}(x)=\dfrac{u^{'}(x)}{2\sqrt{u(x)}}$.
Posons $f$ définie sur $I$ par $f(x)=\sqrt{u(x)}$ $=v\circ u(x)$, avec $v(x)=\sqrt{x}$.
Nous savons que la fonction $v$ est dérivable sur $]0;+\infty[$ et pour tout $x\in I$, $u(x)\in]0;+\infty[$. Les conditions du théorème sur la dérivation d'une fonction composée sont vérifiées.
On a donc $f'(x)=v'[u(x)]\times u'(x)$, or $v'(y)=\dfrac{1}{2\sqrt{y}}$ pour tout $y>0$.
Donc $f'(x)=\dfrac{1}{2\sqrt{u(x)}}\times u'(x)$ $=\dfrac{u^{'}(x)}{2\sqrt{u(x)}}$.
Exercice.
Calculer la fonction dérivée de $f$ sur l'intervalle $I$ donné:
Dérivation de $x\to u(x)^n$, avec $n\in\mathbb{Z}$ et $n\not=-1$.
Exercice.
Calculer la fonction dérivée de $f$ sur l'intervalle $I$ donné:
Définitions.
Exercice.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^5+x^4+x^3+10x+5$; calculer $f^{(4)}(x)$, (la dérivée quatrième de $f$).
Fonctions convexes, concaves.
Convexe.
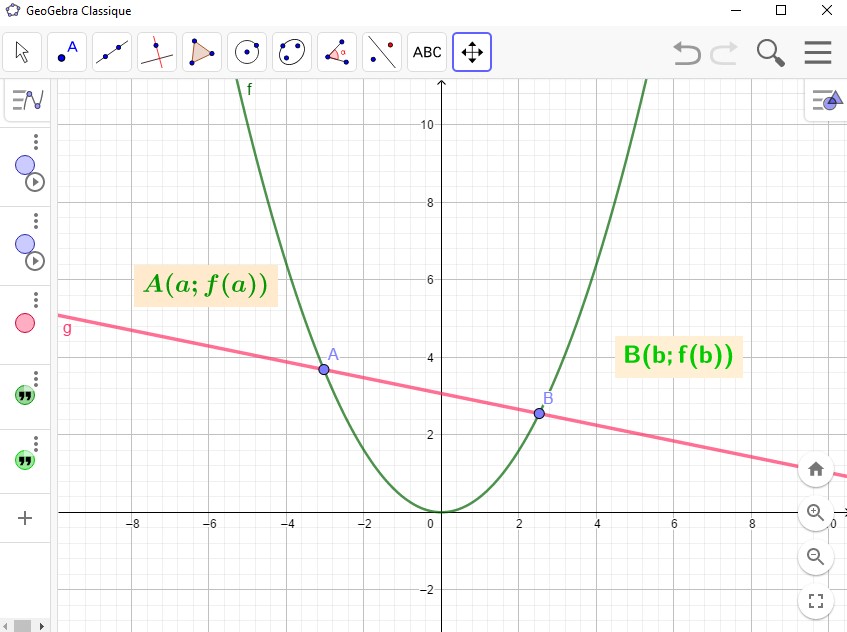
Concave.
Reformulation analytique des définitions de convexité.
Proposition.
Soit $f$ une fonction définie et deux fois dérivable sur un intervalle $I$. les assertions suivantes sont équivalentes:
Exercice.
Soit $g$ la fonction définie sur $\mathbb{R}-\{1\}$ par $f(x)=\dfrac{x+2}{x-1}$.
Définition.
Un point d'inflexion est un point où la courbe représentative d'une fonction traverse sa tangente.
Lorsque la courbe $\mathcal{C}_f$ d'une fonction $f$
admet un point d'inflexion, la fonction change de convexité.
Proposition.
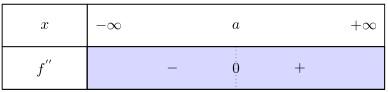
Soit $f$ une fonction deux fois dérivable sur un intervalle $I$.
La courbe $\mathcal{C}_f$ représentative de la fonction $f$ admet un point d'inflexion au point d'abscisse $a$ si et seulemnt si $f^{''}$ s'annule en changeant de signe en $a$.

Exercice.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\dfrac{1}{4}x^4-x^3+10x+4$.