Droites et plans de l'espace.
Caractérisation vectorielle d'une droite dans l'espace.
- Soit $A$, $B$ deux points distincts de l'espace, la droite $(AB)$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=t\overrightarrow{AB}$.
- Soit $A$ un points de l'espace et $\overrightarrow{u}$ un vecteur, la droite passant par $A$ de vecteur directeur $\overrightarrow{u}$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=t\overrightarrow{u}$.
- Le segment $[AB]$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=t\overrightarrow{AB}$ avec $t\in[0;1]$.
- la demi-droite $[AB)$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=t\overrightarrow{AB}$ avec $t\in[0;+\infty[$.
Représentations paramétriques d'une droite.
- Soit $(d)$ la droite passant par $A(2;-3;-1)$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix}-2\\1\\3\\ \end{pmatrix}$, donner une équation paramétrique de $(d)$.
- Le point $C(-2;-1;5)$ appartiennent-il à la droite $(d)$?
- Le point $D(-6;-4;9)$ appartiennent-il à la droite $(d)$?
- $(d):\Bigg\{ \begin{array}[pos]{c} x=-2t+2\\ y=t-3\\ z=3t-1\\ \end{array}$ avec $t\in\mathbb{R}$.
- Recherchons un réel $t$ pour que $\Bigg\{
\begin{array}[pos]{c}
-2t+2=-2\\
t-3=-1\\
3t-1=5\\
\end{array}$.
Pour résoudre ce systéme il suffit de résoudre une des trois équations puis de vérifier les deux autres. Prenons $-2t+2=-2$ $\Leftrightarrow$ $t=2$. Avec $t=2$ les deux autres équations sont bien vérifiées. Donc $C\in(d)$. - $\Bigg\{
\begin{array}[pos]{c}
-2t+2=-6\\
t-3=-4\\
3t-1=9\\
\end{array}$.
Pour résoudre ce systéme il suffit de résoudre une des trois équations puis de vérifier les deux autres. Prenons $-2t+2=-6$ $\Leftrightarrow$ $t=4$. Avec $t=2$ il est clair que $t-3\not=-4$ par exemple, donc le point $D\not\in(d)$. Caractérisation vectorielle d'un plan dans l'espace.
- Soit $A$, $B$, $C$ trois points distincts de l'espace, le plan $(ABC)$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=x\overrightarrow{AB}+y\overrightarrow{AC}$ où $x\in\mathbb{R}$ et $y\in\mathbb{R}$.
- Soit $A$ un point de l'espace, et soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs non colinéaires de l'espace le plan $\mathcal{P}$ passant par $A$ et dirigé par les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}=x\overrightarrow{u}+y\overrightarrow{v}$ où $x\in\mathbb{R}$ et $y\in\mathbb{R}$.
- Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$,et $\overrightarrow{w}$ sont coplanaires si, et seulement si, il existe trois réels $a$, $b$ et $c$
non tous nuls tels que:
$a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$. - Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$,et $\overrightarrow{w}$ ne sont pas coplanaires si, et seulement si, l'assertion suivante est vérifiée:
$a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$ implique $a=b=c=0$. - Si la proposition 1 est vraie alors la deuxiéme est la négation de 2
Rappel de logique
$A\Leftrightarrow B$ veut aussi dire $non(A)\Leftrightarrow non(B)$. - Démontrons la proposition 1:
- Démontrons que si il existe trois réels $a$, $b$ et $c$ non tous nuls tels que $a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$
$\leftrightarrow$ $\overrightarrow{u}$, $\overrightarrow{v}$,et $\overrightarrow{w}$ sont coplanaires.
supposons que $a\not=0$ alors $\overrightarrow{u}=\dfrac{-b}{a}\overrightarrow{v}-\dfrac{c}{b}\overrightarrow{w}$, donc $\leftrightarrow$ $\overrightarrow{u}$, $\overrightarrow{v}$,et $\overrightarrow{w}$ sont coplanaires. - Démontrons la réciproque.
Supposons que $\overrightarrow{v}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ soient coplanaires.
Premier cas
- Démontrons que si il existe trois réels $a$, $b$ et $c$ non tous nuls tels que $a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$
$\leftrightarrow$ $\overrightarrow{u}$, $\overrightarrow{v}$,et $\overrightarrow{w}$ sont coplanaires.
- Soit $\overrightarrow{u}\begin{pmatrix}1\\-3\\5\\ \end{pmatrix}$, $\overrightarrow{v}\begin{pmatrix}4\\1\\1\\ \end{pmatrix}$ et
$\overrightarrow{w}\begin{pmatrix}0\\1\\1\\ \end{pmatrix}$.
Montrer que $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ ne sont pas coplanaires. - Considérons les points $A(1;0;1)$, $B(2;2;4)$, $C(3;0;5)$ et $D(5;-4;7)$. Démontrer que les points $A$, $B$, $C$ et $D$ sont coplanaires.
- Soit trois réls $a$, $b$ et $c$ tels que $a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$.
Nous avons $a\overrightarrow{u}+b\overrightarrow{v}+c\overrightarrow{w}=\overrightarrow{0}$ $\Leftrightarrow$ $\Bigg\{\begin{array}[pos]{c}a+4b=0\\-3a+b+c=0\\5a+b+c=0\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{\begin{array}[pos]{c}a=-4b\\13b+c=0\\-19b+c=0\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{\begin{array}[pos]{c}a=-4b\\c=-13b\\-32b=0\\ \end{array}$ $\Leftrightarrow$ $a=b=c=0$. Donc les vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ ne sont pas coplanaires. - $\overrightarrow{AB}\begin{pmatrix}1\\2\\3\\ \end{pmatrix}$, $\overrightarrow{AC}\begin{pmatrix}2\\0\\4\\ \end{pmatrix}$ et
$\overrightarrow{AD}\begin{pmatrix}4\\-4\\6\\ \end{pmatrix}$. Comme les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$
ne sont pas colinéaires, démontrer que $A(1;0;1)$, $B(2;2;4)$, $C(3;0;5)$ et $D(5;-4;7)$ sont coplanaires revient à montrer qu'il existe deux réels $\alpha$ et $\beta$
tels que $\overrightarrow{AD}=\alpha\times\overrightarrow{AB}+\beta\times\overrightarrow{AC}$.
Donc on a: $\Bigg\{\begin{array}[pos]{c}\alpha+2\beta=4\\2\alpha=-4\\3\alpha+4\beta=6\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{\begin{array}[pos]{c}-2+2\beta=4\\\alpha=-2\\3\alpha+4\beta=6\\ \end{array}$ $\Leftrightarrow$ $\alpha=-2$ et $\beta=3$.
Donc $\overrightarrow{AD}=-2\times\overrightarrow{AB}+3\times\overrightarrow{AC}$, les vecteurs $\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\overrightarrow{AD}$ sont coplanaires et donc il en est de même pour les points $A(1;0;1)$, $B(2;2;4)$, $C(3;0;5)$ et $D(5;-4;7)$. - Une droite $\mathcal{D}$ est parallèle à un plan $\mathcal{P}$ si, et seulement si, un vecteur directeur de $\mathcal{D}$ est coplanaire avec deux vecteurs non colinéaires de $\mathcal{P}$.
- Deux plans $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles si, et seulement si, deux vecteurs non colinéaires du plan $\mathcal{P}$ sont respectivement égaux à deux vecteurs du plan $\mathcal{P}'$.
Représentations paramétriques d'un plan.
- $(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=-2t+t'+2\\ y=t-3\\ z=3t-t'-1\\ \end{array}$ avec $t\in\mathbb{R}$ et $t\in\mathbb{R}$ .
- Recherchons un réel $t$ et $t'$pour que $\Bigg\{
\begin{array}[pos]{c}
-2t+t'+2=-2\\
t-3=-1\\
3t-t'-1=5\\
\end{array}$.
$\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-2\\ t-3=-1\\ 3t-t'-1=5\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-2\\ t=2\\ 6-t'-1=5\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-2\\ t=2\\ t'=0\\ \end{array}$.
Il reste à vérifier la premiére équation du systéme: on a bien $-2\times 2+0+2=-2$. Donc le point $C\in\mathcal{P}$. Le point $C$ est le point du plan de paramétres $t=2$ et $t'=0$. - Recherchons un réel $t$ et $t'$pour que $\Bigg\{
\begin{array}[pos]{c}
-2t+t'+2=-6\\
t-3=-4\\
3t-t'-1=9\\
\end{array}$.
$\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-6\\ t-3=-4\\ 3t-t'-1=9\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-2\\ t=-1\\ -3-t'-1=5\\ \end{array}$ $\Leftrightarrow$ $\Bigg\{ \begin{array}[pos]{c} -2t+t'+2=-2\\ t=-1\\ t'=-9\\ \end{array}$.
Il reste à vérifier la premiére équation du systéme: $-2t+t'+2=2+(-9)+2=-5\not=-2$ donc $D\not\in\mathcal{P}$ - Soit $(\mathcal{P})$ le plan passant par $A(2;-3;-1)$ et de vecteurs directeurs $\overrightarrow{u}\begin{pmatrix}-2\\1\\3\\ \end{pmatrix}$ et $\overrightarrow{u}\begin{pmatrix}1\\0\\-1\\ \end{pmatrix}$ , donner une équation paramétrique de $(\mathcal{P})$.
- Le point $C(-2;-1;5)$ appartiennent-il au plan $(\mathcal{P})$?
- Le point $D(-6;-4;9)$ appartiennent-il au plan $(\mathcal{P})$?
Intersection d'une droite et d'un plan.
Configuration entre une droite $\Delta$ et un plan $\mathcal{P}$.
$\Delta$ et $\mathcal{P}$ sont sécants en un point $I$.
Exercice:
Soit $\mathcal{P}$ le plan et $\mathcal{D}$ la droite de représentation paramétriques respectives:
$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+t\\ y=3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=6-k \\y=-4+2k\\z=1+k \\ \end{array}$ avec $k\in\mathbb{R}$.- Le point A de paramétre 0 de $\mathcal{D}$ appartient-il au plan $\mathcal{P}$?
- Démontrer que la droite $\mathcal{D}$ est sécante au plan $\mathcal{P}$.
$\Delta$ est contenue dans $\mathcal{P}$.
Exercice:
Soit $\mathcal{P}$ le plan et $\mathcal{D}$ la droite de représentation paramétriques respectives:
$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+t\\ y=3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=1-k \\y=3\\z=4-k \\ \end{array}$ avec $k\in\mathbb{R}$.
Démontrer que la droite $\mathcal{D}$ est contenue dans le plan $\mathcal{P}$.$\delta$ et $\mathcal{P}$ sont disjoints.
Exercice:
Soit $\mathcal{P}$ le plan et $\mathcal{D}$ la droite de représentation paramétriques respectives:
$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+t\\ y=3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
$(\mathcal{D}):\Bigg\{\begin{array}[pos]{c}x=1-2k \\y=3\\z=6-2k \\ \end{array}$ avec $k\in\mathbb{R}$.
Démontrer que la droite $\mathcal{D}$ est contenue dans le plan $\mathcal{P}$.Intersection de deux plans.
Définition.
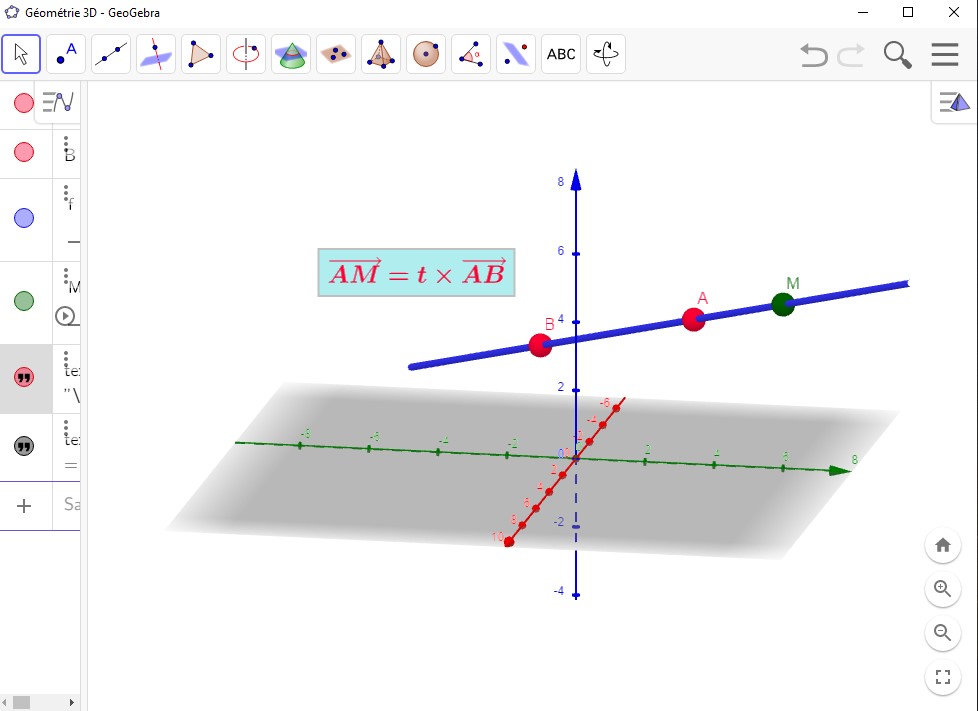
Théorème.
La droite $(d)$ passant par le point $A(x_0;y_0;z_0)$ et de vecteur directeur $\overrightarrow{u}(a;b;c)$ est l'ensemble des points $M(x;y;z)$ tels que: $\Bigg\{ \begin{array}[pos]{c} x=at+x_0\\ y=bt+y_0\\ z=ct+z_0\\ \end{array}$ avec $t\in\mathbb{R}.$
$M(x;y;z)\in(d)$ $\Leftrightarrow$ $\overrightarrow{AM}$ et $\overrightarrow{u}$ sont colinéaire $\Leftrightarrow$
Il existe $t\in\mathbb{R}$ tel que $\overrightarrow{AM}=t\overrightarrow{u}$ $\Leftrightarrow$ $\overrightarrow{AM}\begin{pmatrix}
x-x_A\\
y-y_A\\
z-z_A\\
\end{pmatrix}$ $=t\times\begin{pmatrix}a\\b\\c\\ \end{pmatrix}$ $=\begin{pmatrix}ta\\tb\\tc\\ \end{pmatrix}$.
Donc nous avons donc la relation: $\Bigg\{ \begin{array}[pos]{c} x=at+x_0\\ y=bt+y_0\\ z=ct+z_0\\ \end{array}$ avec $t\in\mathbb{R}$.
Donc nous avons donc la relation: $\Bigg\{ \begin{array}[pos]{c} x=at+x_0\\ y=bt+y_0\\ z=ct+z_0\\ \end{array}$ avec $t\in\mathbb{R}$.
Exercices:
Définition.
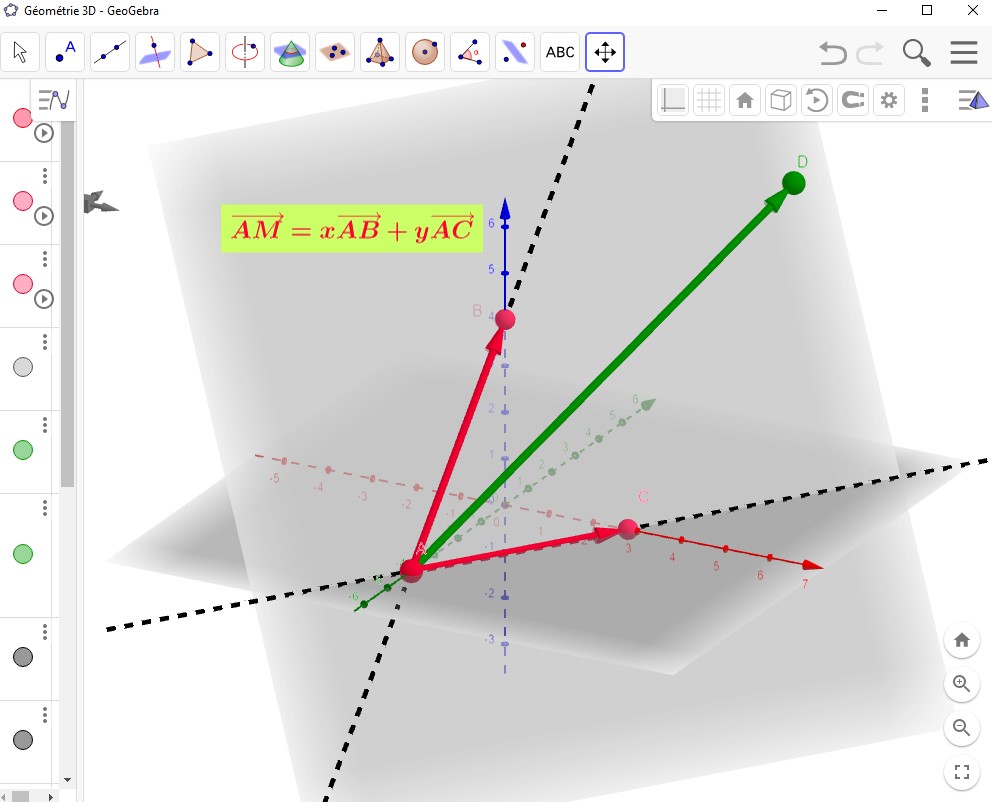
Vecteurs coplanaires.
Des vecteurs sont coplanaires si et seulement si leurs représentants de même origine, un point $A$, ont leurs extrémités dans un même plan passant par A.
Propriétés.
Exercice.
Propriété.
Théorème.
Soit $A(x_0,y_0,z_0)$ un point de l'espace, et soit $\overrightarrow{u}(a,b,c)$ et $\overrightarrow{v}(a',b',c')$ deux vecteurs non colinéaires de l'espace, et le plan $\mathcal{P}$ passant par $A$, dirigé par les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$. Un point $M(x,y,z)$ appartient à $\mathcal{P}$ si et seulement si il existe deux reéls $t$ et $t'$ tels que: $\Bigg\{ \begin{array}[pos]{c} x=at+a't'+x_0\\ y=bt+b't'+y_0\\ z=ct+c't'+z_0\\ \end{array} $.
$M(x,y)$ appartient à $\mathcal{P}$ si et seulement si il existe deux reéls $t$ et $t'$
tels que $\overrightarrow{AM}=t\overrightarrow{u}+t^{'}\overrightarrow{v}$ $\Leftrightarrow$
$\overrightarrow{AM}\begin{pmatrix}
x-x_A\\
y-y_A\\
z-z_A\\
\end{pmatrix}$ $=t\times\begin{pmatrix}a\\b\\c\\ \end{pmatrix}+t^{'}\times\begin{pmatrix}a'\\b'\\c'\\ \end{pmatrix}$
$=\begin{pmatrix}ta+t'a'\\tb+t'b'\\tc+t'c'\\ \end{pmatrix}$.
Donc nous avons donc la relation: $\Bigg\{ \begin{array}[pos]{c} x=at+a't'+x_0\\ y=bt+b't'+y_0\\ z=ct+c't'+z_0\\ \end{array} $.
Donc nous avons donc la relation: $\Bigg\{ \begin{array}[pos]{c} x=at+a't'+x_0\\ y=bt+b't'+y_0\\ z=ct+c't'+z_0\\ \end{array} $.
Exercices.
Configuration entre une droite $\Delta$ et un plan $\mathcal{P}$.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont confondus.
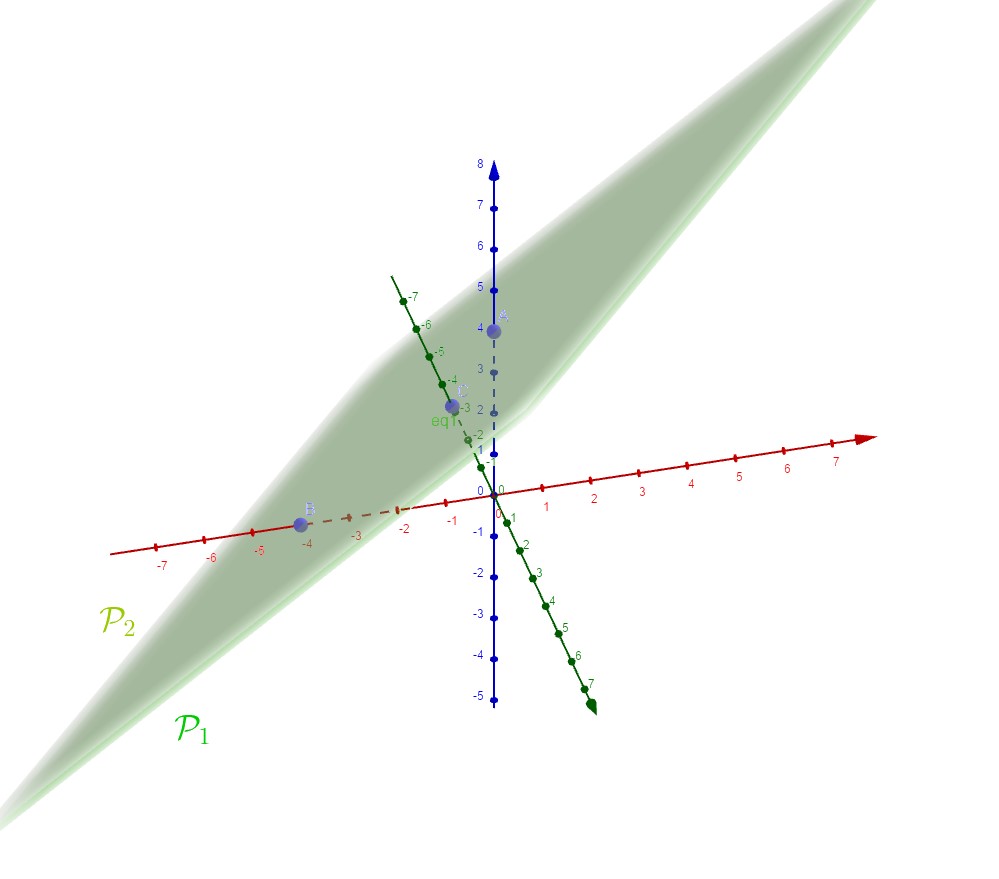
$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+t\\ y=3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+2s \\y=3-2s'\\z=4+2s-4s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont confondus.

Exercice:
Soit $\mathcal{P}$ et $\mathcal{P'}$ deux plans de représentation paramétriques respectives:$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+t\\ y=3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+2s \\y=3-2s'\\z=4+2s-4s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont confondus.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont disjoints.
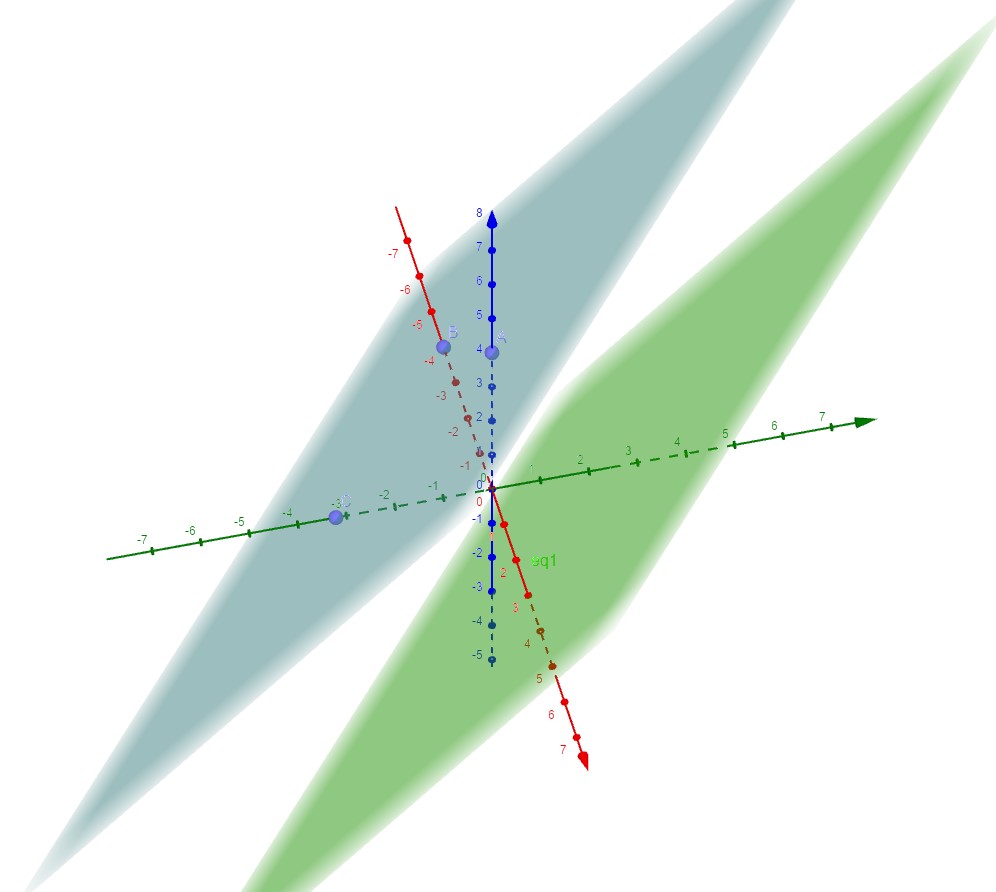
$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=-1+t\\ y=-3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+2s \\y=3-2s'\\z=4+2s-4s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont stictements paralléles.

Exercice:
Soit $\mathcal{P}$ et $\mathcal{P'}$ deux plans de représentation paramétriques respectives:$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=-1+t\\ y=-3+t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+2s \\y=3-2s'\\z=4+2s-4s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont stictements paralléles.
$\mathcal{P}_1$ et $\mathcal{P}_2$ sont sécants.

$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+2t\\ y=3-t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+s \\y=3-2s'\\z=4+2s-3s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont sécants.

Exercice:
Soit $\mathcal{P}$ et $\mathcal{P'}$ deux plans de représentation paramétriques respectives:$(\mathcal{P}):\Bigg\{ \begin{array}[pos]{c} x=1+2t\\ y=3-t'\\ z=4+t+2t'\\ \end{array}$ avec $(t;t')\in\mathbb{R}^2$
et $(\mathcal{P'}):\Bigg\{\begin{array}[pos]{c}x=1+s \\y=3-2s'\\z=4+2s-3s' \\ \end{array}$ avec $(s;s')\in\mathbb{R}^2$.
Démontrer que les plans $\mathcal{P}$ et $\mathcal{P'}$ sont sécants.